Ellipse 1 Question 3
3. Let $S$ and $S^{\prime}$ be the foci of an ellipse and $B$ be any one of the extremities of its minor axis. If $\Delta S^{\prime} B S$ is a right angled triangle with right angle at $B$ and area $\left(\Delta S^{\prime} B S\right)=8 sq$ units, then the length of a latus rectum of the ellipse is
(a) $2 \sqrt{2}$
(b) $4 \sqrt{2}$
(c) 2
(d) 4
(2019 Main, 12 Jan II)
Show Answer
Answer:
Correct Answer: 3. (d)
Solution:
- Let the ellipse be $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$.
Then, according to given information, we have the following figure.
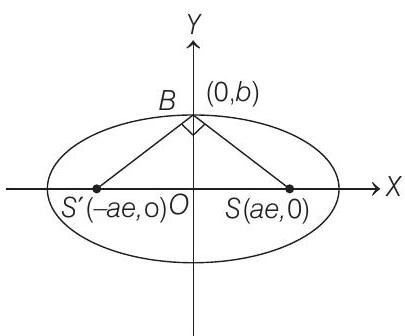
Clearly, slope of line $S B=\frac{b}{-a e}$ and slope of line $S^{\prime} B=\frac{b}{a e}$
$\because$ Lines $S B$ and $S^{\prime} B$ are perpendicular, so
$$ \frac{b}{-a e} \cdot \frac{b}{a e}=-1 $$
$[\because$ product of slopes of two
$$ \Rightarrow \quad b^{2}=a^{2} e^{2} $$
Also, it is given that area of $\Delta S^{\prime} B S=8$
$\therefore \quad \frac{1}{2} a^{2}=8$
$$ \left[\because S^{\prime} B=S B=a \text { because } S^{\prime} B+S B=2 a \text { and } S^{\prime} B=S B\right] $$
$\Rightarrow \quad a^{2}=16 \Rightarrow a=4$
$\because \quad e^{2}=1-\frac{b^{2}}{a^{2}}=1-e^{2}$
[from Eq. (i)]
$\Rightarrow \quad 2 e^{2}=1$
$\Rightarrow \quad e^{2}=\frac{1}{2}$
From Eqs. (i) and (iii), we get
$$ \begin{array}{cc} & b^{2}=a^{2} \frac{1}{2}=16 \frac{1}{2} \quad \text { [using Eq. (ii)] } \\ \Rightarrow \quad & b^{2}=8 \end{array} $$
Now, length of latus rectum $=\frac{2 b^{2}}{a}=\frac{2 \times 8}{4}=4$ units
4 Let the equation of ellipse be $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$
Then, according the problem, we have
$$ \frac{2 b^{2}}{a}=8 \text { and } 2 a e=2 b $$
$$ \text { [Length of latusrectum }=\frac{2 b^{2}}{a} \text { and } $$
length of minor axis $=2 b]$
$$ \begin{aligned} & \Rightarrow \quad b \frac{b}{a}=4 \text { and } \frac{b}{a}=e \\ & \Rightarrow \quad b(e)=4 \\ & \Rightarrow \quad b=4 \cdot \frac{1}{e} \end{aligned} $$
Also, we know that $b^{2}=a^{2}\left(1-e^{2}\right)$
$$ \begin{array}{rlrlrl} \Rightarrow & & \frac{b^{2}}{a^{2}}=1 & -e^{2} & \Rightarrow e^{2}=1-e^{2} & \\ \Rightarrow & 2 e^{2} & =1 & & \\ \Rightarrow & & e & =\frac{1}{\sqrt{2}} & \end{array} $$
From Eqs. (i) and (ii), we get
Now, $\quad a^{2}=\frac{b^{2}}{1-e^{2}}=\frac{32}{1-\frac{1}{2}}=64$
$\therefore$ Equation of ellipse be $\frac{x^{2}}{64}+\frac{y^{2}}{32}=1$
Now, check all the options.
Only $(4 \sqrt{3}, 2 \sqrt{2})$, satisfy the above equation.
