Ellipse 1 Question 13
14. If the tangents to the ellipse at $M$ and $N$ meet at $R$ and the normal to the parabola at $M$ meets the $X$-axis at $Q$, then the ratio of area of $\triangle M Q R$ to area of the quadrilateral $M F _1 N F _2$ is
(a) $3: 4$
(b) $4: 5$
(c) $5: 8$
(d) $2: 3$
Show Answer
Answer:
Correct Answer: 14. (c)
Solution:
- Equation of tangent at $M(3 / 2, \sqrt{6})$ to $\frac{x^{2}}{9}+\frac{y^{2}}{8}=1$ is
$$ \frac{3}{2} \cdot \frac{x}{9}+\sqrt{6} \cdot \frac{y}{8}=1 $$
which intersect $X$-axis at $(6,0)$.
Also, equation of tangent at $N(3 / 2,-\sqrt{6})$ is
$$ \frac{3}{2} \cdot \frac{x}{9}-\sqrt{6} \frac{y}{8}=1 $$
Eqs. (i) and (ii) intersect on $X$-axis at $R(6,0)$.
Also, normal at $M(3 / 2, \sqrt{6})$ is $y-\sqrt{6}=\frac{-\sqrt{6}}{2} \quad x-\frac{3}{2}$
On solving with $y=0$, we get $Q(7 / 2,0)$
$\therefore \quad$ Area of $\triangle M Q R=\frac{1}{2} \quad 6-\frac{7}{2} \quad \sqrt{6}=\frac{5 \sqrt{6}}{4}$ sq units
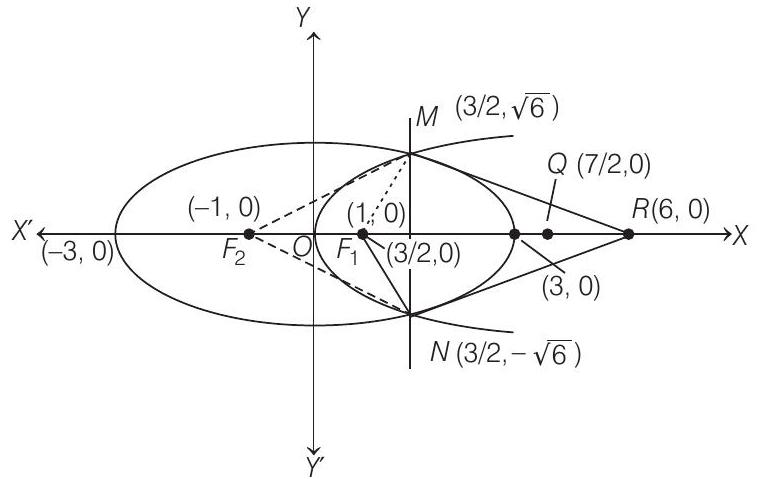
and area of quadrilateral $M F _1 N F _2=2 \times \frac{1}{2}{1-(-1)} \sqrt{6}$
$\therefore \frac{\text { Area of } \triangle M Q R}{\text { Area of quadrilateral } M F _1 N F _2}=\frac{5}{8}$ $=2 \sqrt{6}$ sq units
