Differential Equations 3 Question 6
6. A solution curve of the differential equation $\left(x^{2}+x y+4 x+2 y+4\right) \frac{d y}{d x}-y^{2}=0, x>0$, passes through the point $(1,3)$. Then, the solution curve
(2016 Adv.)
(a) intersects $y=x+2$ exactly at one point
(b) intersects $y=x+2$ exactly at two points
(c) intersects $y=(x+2)^{2}$
(d) does not intersect $y=(x+3)^{2}$
Show Answer
Answer:
Correct Answer: 6. (a, d)
Solution:
- Given,
$$ \left(x^{2}+x y+4 x+2 y+4\right) \frac{d y}{d x}-y^{2}=0 $$
$\Rightarrow \quad\left[\left(x^{2}+4 x+4\right)+y(x+2)\right] \frac{d y}{d x}-y^{2}=0$
$$ \Rightarrow \quad\left[(x+2)^{2}+y(x+2)\right] \frac{d y}{d x}-y^{2}=0 $$
Put $x+2=X$ and $y=Y$, then
$$ \begin{array}{rlrl} & & \left(X^{2}+X Y\right) \frac{d Y}{d X}-Y^{2} & =0 \\ \Rightarrow & X^{2} d Y+X Y d Y-Y^{2} d X & =0 \\ \Rightarrow & X^{2} d Y+Y(X d Y-Y d X) & =0 \\ \Rightarrow & -\frac{d Y}{Y} & =\frac{X d Y-Y d X}{X^{2}} \\ \Rightarrow & -d(\log |Y|) & =d \frac{Y}{X} \end{array} $$
On integrating both sides, we get
$$ \begin{aligned} -\log |Y| & =\frac{Y}{X}+C, \text { where } x+2=X \text { and } y=Y \\ \Rightarrow \quad-\log |y| & =\frac{y}{x+2}+C \end{aligned} $$
Since, it passes through the point $(1,3)$.
$$ \begin{array}{rlrl} \therefore & & -\log 3 & =1+C \\ \Rightarrow & & C & =-1-\log 3=-(\log e+\log 3) \\ & & =-\log 3 e \end{array} $$
$\therefore$ Eq. (i) becomes
$$ \begin{array}{ll} & \log |y|+\frac{y}{x+2}-\log (3 e)=0 \\ \Rightarrow \quad & \log \frac{|y|}{3 e}+\frac{y}{x+2}=0 \end{array} $$
Now, to check option (a), $y=x+2$ intersects the curve.
$$ \begin{array}{ll} \Rightarrow & \log \frac{|x+2|}{3 e}+\frac{x+2}{x+2}=0 \Rightarrow \log \frac{|x+2|}{3 e}=-1 \\ \Rightarrow & \frac{|x+2|}{3 e}=e^{-1}=\frac{1}{e} \\ \Rightarrow & |x+2|=3 \text { or } x+2= \pm 3 \end{array} $$
$\therefore x=1,-5$ (rejected), as $x>0$
[given]
$\therefore x=1$ only one solution.
Thus, (a) is the correct answer.
To check option (c), we have
$$ \begin{gathered} y=(x+2)^{2} \text { and } \log \frac{|y|}{3 e}+\frac{y}{x+2}=0 \\ \Rightarrow \log \frac{|x+2|^{2}}{3 e}+\frac{(x+2)^{2}}{x+2}=0 \Rightarrow \log \frac{|x+2|^{2}}{3 e}=-(x+2) \\ \Rightarrow \frac{(x+2)^{2}}{3 e}=e^{-(x+2)} \text { or }(x+2)^{2} \cdot e^{x+2}=3 e \Rightarrow e^{x+2}=\frac{3 e}{(x+2)^{2}} \\ \text { 3e/(x+2) } x e^{x+2} x \end{gathered} $$
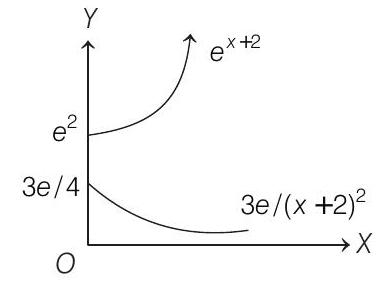
Clearly, they have no solution.
To check option (d), $y=(x+3)^{2}$
i.e. $\quad \log \frac{|x+3|^{2}}{3 e}+\frac{(x+3)^{2}}{(x+2)}=0$
To check the number of solutions.
Let $g(x)=2 \log (x+3)+\frac{(x+3)^{2}}{(x+2)}-\log (3 e)$
$\therefore \quad g^{\prime}(x)=\frac{2}{x+3}+\frac{(x+2) \cdot 2(x+3)-(x+3)^{2} \cdot 1}{(x+2)^{2}}-0$
$=\frac{2}{x+3}+\frac{(x+3)(x+1)}{(x+2)^{2}}$
Clearly, when $x>0$, then, $g^{\prime}(x)>0$
$\therefore \quad g(x)$ is increasing, when $x>0$.
Thus, $\quad$ when $x>0$, then $g(x)>g(0)$
$$ g(x)>\log \frac{3}{e}+\frac{9}{4}>0 $$
Hence, there is no solution. Thus, option (d) is true.
