Differential Equations 3 Question 10
10. A right circular cone with radius $R$ and height $H$ contains a liquid which evaporates at a rate proportional to its surface area in contact with air (proportionality constant $=k>0$ ). Find the time after which the cone is empty.
$(2003,4$ M)
Show Answer
Answer:
Correct Answer: 10. $T=\frac{H}{k}$
Solution:
- Given, liquid evaporates at a rate proportional to its surface area.
$\Rightarrow \quad \frac{d V}{d t} \propto-S$
We know that, volume of cone $=\frac{1}{3} \pi r^{2} h$
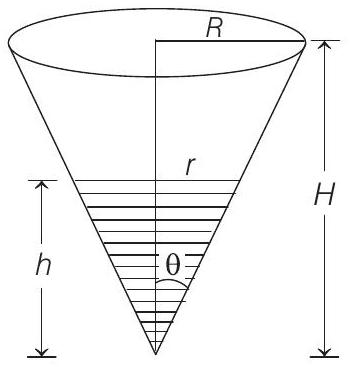
and surface area $=\pi r^{2}$
or $\quad V=\frac{1}{3} \pi r^{2} h \quad$ and $\quad S=\pi r^{2}$
Where,
$$ \tan \theta=\frac{R}{H} \quad \text { and } \quad \frac{r}{h}=\tan \theta $$
From Eqs. (ii) and (iii), we get
$$ V=\frac{1}{3} \pi r^{3} \cot \theta \text { and } S=\pi r^{2} $$
On substituting Eq. (iv) in Eq. (i), we get
$$ \begin{array}{rlrl} & & \frac{1}{3} \cot \theta \cdot 3 r^{2} \frac{d r}{d t} & =-k \pi r^{2} \\ \Rightarrow & & \cot \theta \int _R^{0} d r & =-k \int _0^{T} d t \\ \Rightarrow & & \cot \theta(0-R) & =-k(T-0) \\ \Rightarrow & R \cot \theta & =k T \Rightarrow H=k T \quad \text { [from Eq. (iii)] } \\ \Rightarrow & & T & =\frac{H}{k} \end{array} $$
$\therefore$ Required time after which the cone is empty, $T=\frac{H}{k}$
