Complex Numbers 4 Question 9
9. Suppose $z _1, z _2, z _3$ are the vertices of an equilateral triangle inscribed in the circle $|z|=2$. If $z _1=1+i \sqrt{3}$, then $z _2=\ldots, z _3=\ldots$.
(1994, 2M)
Show Answer
Answer:
Correct Answer: 9. $z _2=-2, z _3=1-i \sqrt{3}$
Solution:
- $z _1=1+i \sqrt{3}=r(\cos \theta+i \sin \theta)$
[let]
$\Rightarrow \quad r \cos \theta=1, r \sin \theta=\sqrt{3}$
$\Rightarrow \quad r=2$ and $\theta=\pi / 3$
So, $\quad z _1=2(\cos \pi / 3+\sin \pi / 3)$
Since, $\quad\left|z _2\right|=\left|z _3\right|=2$
[given]
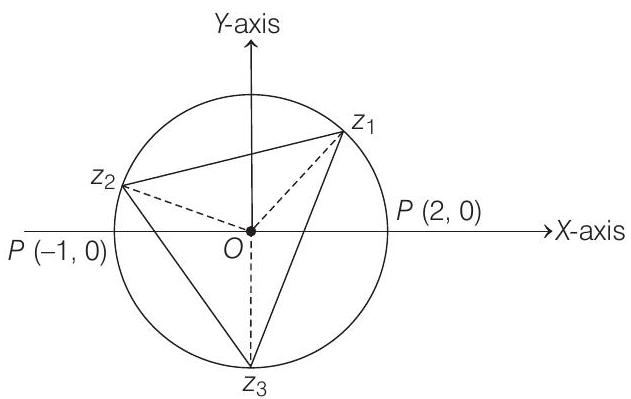
Now, the triangle $z _1, z _2$ and $z _3$ being an equilateral and the sides $z _1 z _2$ and $z _1 z _3$ make an angle $2 \pi / 3$ at the centre.
Therefore, $\quad \angle P O z _2=\frac{\pi}{3}+\frac{2 \pi}{3}=\pi$
and $\quad \angle P O z _3=\frac{\pi}{3}+\frac{2 \pi}{3}+\frac{2 \pi}{3}=\frac{5 \pi}{3}$
Therefore, $z _2=2(\cos \pi+i \sin \pi)=2(-1+0)=-2$
and $z _3=2 \quad \cos \frac{5 \pi}{3}+i \sin \frac{5 \pi}{3}=2 \quad \frac{1}{2}-i \frac{\sqrt{3}}{2}=1-i \sqrt{3}$
Alternate Solution
Whenever vertices of an equilateral triangle having centroid is given its vertices are of the form $z, z \omega, z \omega^{2}$.
$\therefore$ If one of the vertex is $z _1=1+i \sqrt{3}$, then other two vertices are $\left(z _1 \omega\right),\left(z _1 \omega^{2}\right)$.
$$ \begin{array}{lrl} \Rightarrow & (1+i \sqrt{3}) \frac{(-1+i \sqrt{3})}{2},(1+i \sqrt{3}) \frac{(-1-i \sqrt{3})}{2} \\ \Rightarrow & \frac{-(1+3)}{2},-\frac{\left(1+i^{2}(\sqrt{3})^{2}+2 i \sqrt{3}\right)}{2} \\ \Rightarrow & -2,-\frac{(-2+2 i \sqrt{3})}{2}=1-i \sqrt{3} \\ \therefore & z _2=-2 \text { and } z _3=1-i \sqrt{3} \end{array} $$
