Complex Numbers 4 Question 4
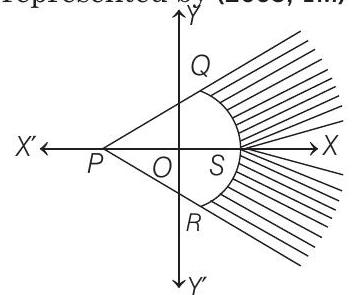
4. The shaded region, where $P=(-1,0), Q=(-1+\sqrt{2}, \sqrt{2})$ $R=(-1+\sqrt{2},-\sqrt{2}), S=(1,0)$ is represented by $(2005,1 M)$
(a) $|z+1|>2,|\arg (z+1)|<\frac{\pi}{4}$
(b) $|z+1|<2,|\arg (z+1)|<\frac{\pi}{2}$
(c) $|z+1|>2$, $|\arg (z+1)|>\frac{\pi}{4}$
(d) $|z-1|<2,|\arg (z+1)|>\frac{\pi}{2}$
Show Answer
Answer:
Correct Answer: 4. (a)
Solution:
- Since, $|P Q|=|P S|=|P R|=2$
$\therefore \quad$ Shaded part represents the external part of circle having centre $(-1,0)$ and radius 2 .
As we know equation of circle having centre $z _0$ and radius $r$, is $\left|z-z _0\right|=r$
$$ \begin{array}{ll} \therefore & |z-(-1+0 i)|>2 \\ \Rightarrow & |z+1|>2 \end{array} $$
Also, argument of $z+1$ with respect to positive direction of $X$-axis is $\pi / 4$.
$$ \therefore \quad \arg (z+1) \leq \frac{\pi}{4} $$
and argument of $z+1$ in anticlockwise direction is $-\pi / 4$.
$$ \therefore \quad \rightarrow \pi / 4 \leq \arg (z+1) $$
From Eqs. (i) and (ii),
$$ |\arg (z+1)| \leq \pi / 4 $$
