Complex Numbers 4 Question 3
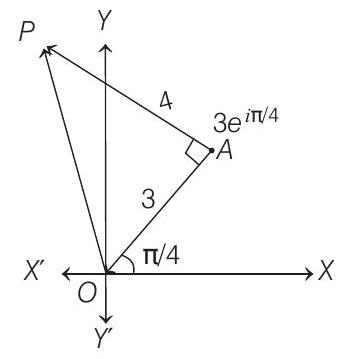
3. A man walks a distance of 3 units from the origin towards the North-East ( $\left.N 45^{\circ} E\right)$ direction. From there, he walks a distance of 4 units towards the North-West $\left(N 45^{\circ} W\right)$ direction to reach a point $P$. Then, the position of $P$ in the Argand plane is
(2007, 3M) $(3+4 i) e^{i \pi / 4}$
(a) $3 e^{i \pi / 4}+4 i$
(b) $(3-4 i) e^{i \pi / 4}$
(c) $(4+3 i) e^{i \pi / 4}$
(d)
Show Answer
Answer:
Correct Answer: 3. (d)
Solution:
- Let $O A=3$, so that the complex number associated with $A$ is $3 e^{i \pi / 4}$. If $z$ is the complex number associated with $P$, then
$$ \begin{aligned} \frac{z-3 e^{i \pi / 4}}{0-3 e^{i \pi / 4}} & =\frac{4}{3} e^{-i \pi / 2}=-\frac{4 i}{3} \\ \Rightarrow \quad 3 z-9 e^{i \pi / 4} & =12 i e^{i \pi / 4} \\ \Rightarrow \quad z & =(3+4 i) e^{i \pi / 4} \end{aligned} $$
