Complex Numbers 4 Question 2
2. A particle $P$ starts from the point $z _0=1+2 i$, where $i=\sqrt{-1}$. It moves first horizontally away from origin by 5 units and then vertically away from origin by 3 units to reach a point $z _1$. From $z _1$ the particle moves $\sqrt{2}$ units in the direction of the vector $\hat{\mathbf{i}}+\hat{\mathbf{j}}$ and then it moves through an angle $\frac{\pi}{2}$ in anti-clockwise direction on a circle with centre at origin, to reach a point $z _2$. The point $z _2$ is given by
(2008, 3M)
(a) $6+7 i$
(b) $-7+6 i$
(c) $7+6 i$
(d) $-6+7 i$
Show Answer
Answer:
Correct Answer: 2. (d)
Solution:
$z _2^{\prime}=\left(6+\sqrt{2} \cos 45^{\circ}, 5+\sqrt{2} \sin 45^{\circ}\right)=(7,6)=7+6 i$
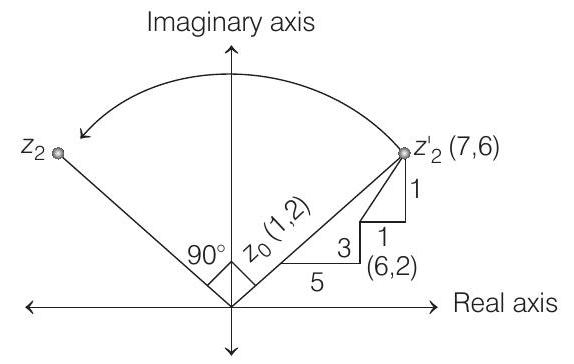
By rotation about $(0,0)$,
$$ \begin{aligned} \frac{z _2}{z _2^{\prime}} & =e^{i \pi / 2} \Rightarrow z _2=z _2^{\prime} e^{i \frac{\pi}{2}} \\ & =(7+6 i) \quad \cos \frac{\pi}{2}+i \sin \frac{\pi}{2}=(7+6 i)(i)=-6+7 i \end{aligned} $$
