Complex Numbers 4 Question 15
15. Complex numbers
(1986,
Show Answer
Solution:
- Since, triangle is a right angled isosceles triangle.
where,
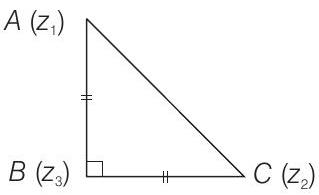
On squaring both sides, we get






