Complex Numbers 3 Question 9
9. Let
(2010)
(a)
(c)
(d)
Match the Columns
Show Answer
Answer:
Correct Answer: 9.
Solution:
- Given,
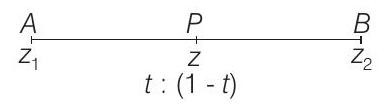
Clearly,
Also,
or
Option (c) is correct.






