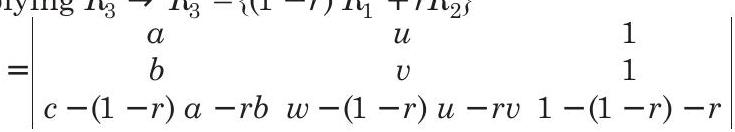Complex Numbers 3 Question 7
7. If $a, b, c$ and $u, v, w$ are the complex numbers representing the vertices of two triangles such that $c=(1-r) a+r b$ and $w=(1-r) u+r v$, where $r$ is a complex number, then the two triangles
$(1985,2 M)$
(a) have the same area
(b) are similar
(c) are congruent
(d) None of these
Objective Questions II
(One or more than one correct option)
Show Answer
Answer:
Correct Answer: 7. (b)
Solution:
- Since $a, b, c$ and $u, v, w$ are the vertices of two triangles.
$$ \begin{aligned} & \text { Also, } \quad c=(1-r) a+r b \\ & \text { and } \quad w=(1-r) u+r v \\ & \begin{array}{lll} a & u & 1 \end{array} \\ & \begin{array}{lll} b & v & 1 \end{array} \\ & c \quad w \quad 1 \end{aligned} $$
$$ \begin{aligned} & =\begin{array}{lll} a & u & 1 \\ b & v & 1 \\ 0 & 0 & 0 \end{array}=0 \end{aligned} $$
