Complex Numbers 1 Question 5
5. Let
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 5. (d)
Solution:
- Let
As
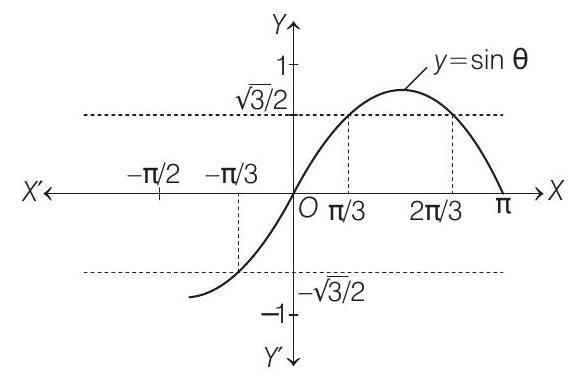
Sum of values of






