Circle 5 Question 7
7. The equations of the tangents drawn from the origin to the circle
(a)
(b)
(c)
(d)
Assertion and Reason
For the following questions, choose the correct answer from the codes (a), (b), (c) and (d) defined as follows.
(a) Statement I is true, Statement II is also true;
Statement II is the correct explanation of Statement I.
(b) Statement I is true, Statement II is also true; Statement II is not the correct explanation of Statement I
(c) Statement I is true; Statement II is false
(d) Statement I is false; Statement II is true
Show Answer
Answer:
Correct Answer: 7.
Solution:
- Since, tangents are drawn from origin. So, the equation of tangent be
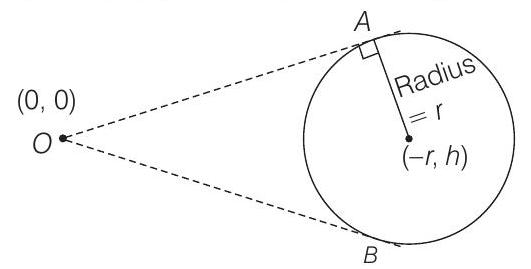
Therefore (a) and (c) are the correct answers.






