Circle 5 Question 6
6. The locus of the mid-point of a chord of the circle $x^{2}+y^{2}=4$ which subtends a right angle at the origin, is
(a) $x+y=2$
(b) $x^{2}+y^{2}=1$
(1984, 2M)
(c) $x^{2}+y^{2}=2$
(d) $x+y=1$
Objective Question II
(One or more than one correct option)
Show Answer
Answer:
Correct Answer: 6. (c)
Solution:
- We have to find locus of mid-point of chord and we know perpendicular from centre bisects the chord.
$$ \therefore \quad \angle O A C=45^{\circ} $$
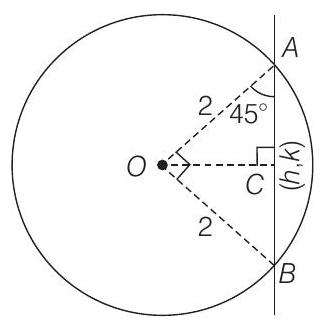
In $\triangle O A C$,
$$ \frac{O C}{O A}=\sin 45^{\circ} $$
$\Rightarrow \quad O C=\frac{2}{\sqrt{2}}=\sqrt{2}$
Also,
$$ \sqrt{h^{2}+k^{2}}=O C^{2} $$
Hence, $x^{2}+y^{2}=2$ is required equation of locus of mid-point of chord subtending right angle at the centre.
