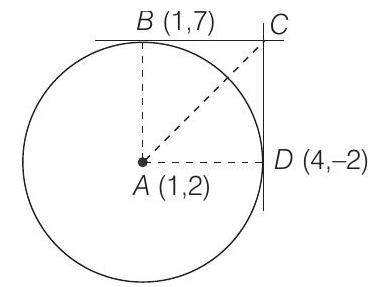
Circle 5 Question 23
23. Let
Integer Answer Type Question
Show Answer
Answer:
Correct Answer: 23. 75 sq units
Solution:
- Equation of tangents at