Circle 5 Question 22
22. Through a fixed point $(h, k)$ secants are drawn to the circle $x^{2}+y^{2}=r^{2}$. Show that the locus of the mid-points of the secants intercepted by the circle is $x^{2}+y^{2}=h x+k y . \quad(1983,5 M)$
Show Answer
Answer:
Correct Answer: 22. $x^{2}+y^{2}=h x+k y$
Solution:
- Given, circle is $x^{2}+y^{2}=r^{2}$
Equation of chord whose mid point is given, is $T=S _1 \Rightarrow x x _1+y y _1-r^{2}=x _1^{2}+y _1^{2}-r^{2}$
It also passes through $(h, k) h x _1+k y _1=x _1^{2}+y _1^{2}$
$\therefore$ Locus of $\left(x _1, y _1\right)$ is
$$ x^{2}+y^{2}=h x+k y $$
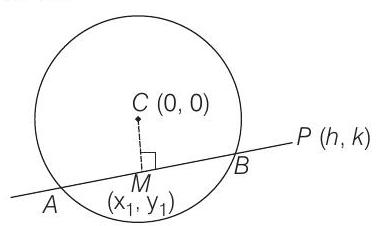
Alternate Solution
Let $M$ be the mid-point of chord $A B$.
$$ \begin{array}{ll} \Rightarrow & C M \perp M P \\ \Rightarrow & \text { (slope of } C M) \cdot(\text { slope of } M P)=-1 \\ \Rightarrow & \frac{y _1}{x _1} \cdot \frac{k-y _1}{h-x _1}=-1 \\ \Rightarrow & k y _1-y _1^{2}=-h x _1+x _1^{2} \\ \text { Hence, required locus is } x^{2}+y^{2}=h x+k y \end{array} $$
