Circle 5 Question 21
21. Lines
(1986, 5M)
Show Answer
Answer:
Correct Answer: 21.
Solution:
- Since,
Let the centre coordinates be
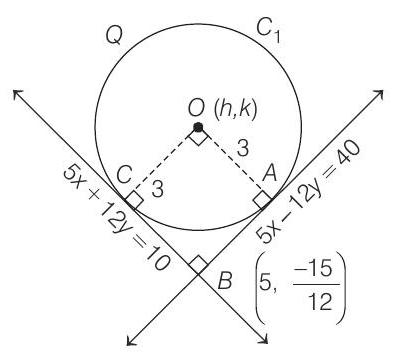
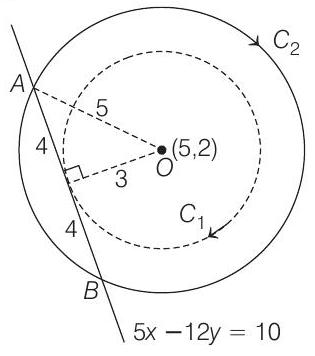
To obtain equation of circle concentric with






