Circle 5 Question 2
2. The sum of the squares of the lengths of the chords intercepted on the circle, $x^{2}+y^{2}=16$, by the lines, $x+y=n, n \in N$, where $N$ is the set of all natural numbers, is
(2019, Main, 8 April I)
(a) 320
(b) 105
(c) 160
(d) 210
Show Answer
Answer:
Correct Answer: 2. (d)
Solution:
- Given equation of line is $x+y=n, n \in N$
and equation of circle is $x^{2}+y^{2}=16$
Now, for intercept, made by circle (ii) with line (i)
$$ \Rightarrow \quad \begin{gathered} d<4 \\ \frac{n}{\sqrt{2}}<4 \end{gathered} $$
$[\because d=$ perpendicular distance from $(0,0)$ to the line $x+y=n$ and it equal to $\frac{|0+0-n|}{\sqrt{1^{2}+1^{2}}}=\frac{n}{\sqrt{2}}$
$$ \Rightarrow \quad n<4 \sqrt{2} $$
$\because n \in N$, so $n=1,2,3,4,5$
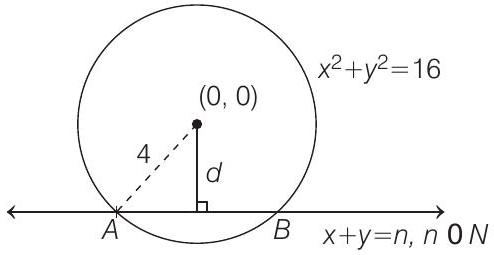
Clearly, length of chord $A B=2 \sqrt{4^{2}-d^{2}}$
$$ =2 \sqrt{16-\frac{n^{2}}{2}} \quad \because d=\frac{n}{\sqrt{2}} $$
$\therefore$ Sum of square of all possible lengths of chords (for $n=1,2,3,4,5$ )
$$ \begin{aligned} & =4 \quad(16 \times 5)-\frac{1}{2}\left(1^{2}+2^{2}+3^{2}+4^{2}+5^{2}\right) \\ & =320-2 \frac{5(6)(11)}{6}=320-110=210 \end{aligned} $$
