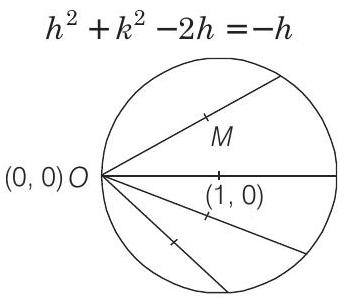
Circle 5 Question 15
15. From the origin chords are drawn to the circle $(x-1)^{2}+y^{2}=1$. The equation of the locus of the mid points of these chords is… .
$(1985,2 M)$
Analytical & Descriptive Questions
Show Answer
Answer:
Correct Answer: 15. $x^{2}+y^{2}-x=0$
Solution:
- For the equation of circle $x^{2}+y^{2}-2 x=0$. Let the mid-point of chords be $(h, k)$.
$\therefore$ Equation of chord bisected at the point is $S _1=T$.
$\therefore h^{2}+k^{2}-2 h=x h+y k-(x+h)$ which passes through $(0,0)$.
$\Rightarrow$
$\therefore$ The required locus of a chord is $x^{2}+y^{2}-x=0$
