Circle 4 Question 7
7. The locus of the centre of circle which touches $(y-1)^{2}+x^{2}=1$ externally and also touches $X$-axis, is
(a) ${x^{2}=4 y, y \geq 0 } \cup{(0, y), y<0}$
(b) $x^{2}=y$
(c) $y=4 x^{2}$
(d) $y^{2}=4 x \cup(0, y), y \in R$
(2005, 2M)
Show Answer
Answer:
Correct Answer: 7. (a)
Solution:
- Let the locus of centre of circle be $(h, k)$ touching $(y-1)^{2}+x^{2}=1$ and $X$-axis shown as
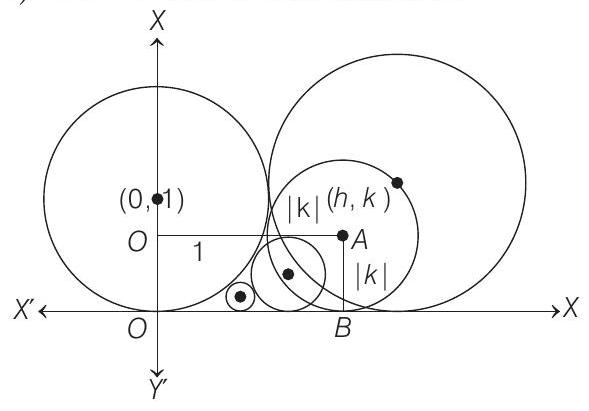
Clearly, from figure,
Distance between $C$ and $A$ is always $1+|k|$,
i.e. $\sqrt{(h-0)^{2}+(k-1)^{2}}=1+|k|$,
$\Rightarrow \quad h^{2}+k^{2}-2 k+1=1+k^{2}+2|k|$
$\Rightarrow \quad h^{2}=2|k|+2 k \Rightarrow x^{2}=2|y|+2 y$
where $\quad|y|=\begin{gathered}y, y \geq 0 \ -y, y<0\end{gathered}$
$\therefore \quad x^{2}=2 y+2 y, y \geq 0$
and $\quad x^{2}=-2 y+2 y, y<0$
$\Rightarrow \quad x^{2}=4 y$, when $y \geq 0$
and $\quad x^{2}=0$, when $y<0$
$\therefore \quad{(x, y): x^{2}=4 y\right.$, when $\left.y \geq 0 } \cup{(0, y): y<0}$
