Circle 4 Question 4
4. Three circles of radii $a, b, c(a<b<c)$ touch each other externally. If they have $X$-axis as a common tangent, then
(2019 Main, 9 Jan I)
(a) $a, b, c$ are in $AP$
(b) $\frac{1}{\sqrt{a}}=\frac{1}{\sqrt{b}}+\frac{1}{\sqrt{c}}$
(c) $\sqrt{a}, \sqrt{b}, \sqrt{c}$ are in AP
(d) $\frac{1}{\sqrt{b}}=\frac{1}{\sqrt{a}}+\frac{1}{\sqrt{c}}$
Show Answer
Answer:
Correct Answer: 4. (b)
Solution:
- According to given information, we have the following figure.
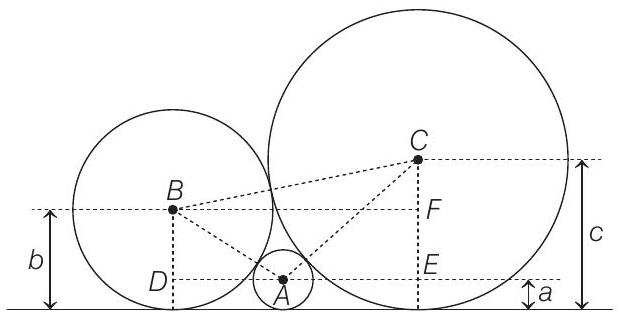
where $A, B, C$ are the centres of the circles Clearly, $A B=a+b$ (sum of radii) and $B D=b-a$
$\therefore A D=\sqrt{(a+b)^{2}-(b-a)^{2}}$
$$ =2 \sqrt{a b} $$
(using Pythagoras theorem in $\triangle A B D$ )
Similarly, $A C=a+c$ and $C E=c-a$
$\therefore$ In $\triangle A C E, A E=\sqrt{(a+c)^{2}-(c-a)^{2}}=2 \sqrt{a c}$
Similarly, $B C=b+c$ and $C F=c-b$
$\therefore \operatorname{In} \triangle B C F, B F=\sqrt{(b+c)^{2}-(c-b)^{2}}=2 \sqrt{b c}$
$\because \quad A D+A E=B F$
$\therefore \quad 2 \sqrt{a b}+2 \sqrt{a c}=2 \sqrt{b c}$
$$ \Rightarrow \quad \frac{1}{\sqrt{c}}+\frac{1}{\sqrt{b}}=\frac{1}{\sqrt{a}} $$
