Circle 4 Question 3
3. Two circles with equal radii are intersecting at the points
(2019 Main, 11 Jan I)
(a)
(b)
(c) 1
(d) 2
Show Answer
Answer:
Correct Answer: 3. (d)
Solution:
- Clearly, circles are orthogonal because tangent at one point of intersection is passing through centre of the other.
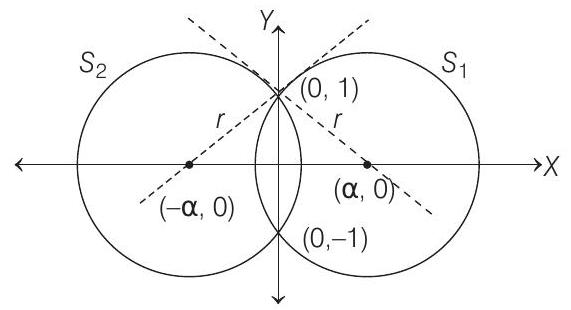
Let
Then,
and






