Circle 4 Question 20
20. Let $S \equiv x^{2}+y^{2}+2 g x+2 f y+c=0$ be a given circle. Find the locus of the foot of the perpendicular drawn from the origin upon any chord of $S$ which subtends a right angle at the origin.
$(1988,5$ M)
Show Answer
Answer:
Correct Answer: 20. $x^{2}+y^{2}+g x+f y+\frac{c}{2}=0$
Solution:
- Let $P(h, k)$ be the foot of perpendicular drawn from origin $O(0,0)$ on the chord $A B$ of the given circle such that the chord $A B$ subtends a right angle at the origin.
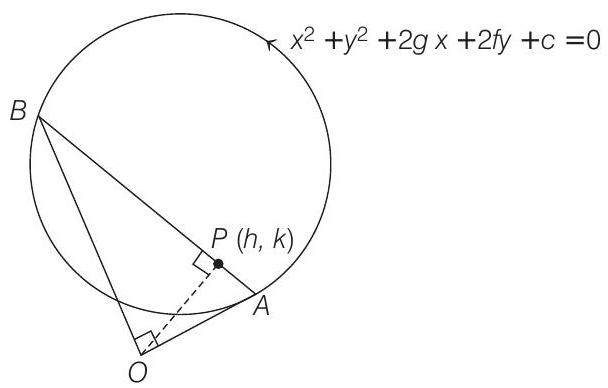
The equation of chord $A B$ is
$$ y-k=-\frac{h}{k}(x-h) \Rightarrow h x+k y=h^{2}+k^{2} $$
The combined equation of $O A$ and $O B$ is homogeneous equation of second degree obtained by the help of the given circle and the chord $A B$ and is given by,
$$ x^{2}+y^{2}+(2 g x+2 f y) \frac{h x+k y}{h^{2}+k^{2}}+c{\frac{h x+k y}{h^{2}+k^{2}}}^{2}=0 $$
Since, the lines $O A$ and $O B$ are at right angle. $\therefore$ Coefficient of $x^{2}+$ Coefficient of $y^{2}=0$
$\Rightarrow 1+\frac{2 g h}{h^{2}+k^{2}}+\frac{c h^{2}}{\left(h^{2}+k^{2}\right)^{2}}$
$$ +1+\frac{2 f k}{h^{2}+k^{2}}+\frac{c k^{2}}{\left(h^{2}+k^{2}\right)^{2}}=0 $$
$\Rightarrow 2\left(h^{2}+k^{2}\right)+2(g h+f k)+c=0$
$\Rightarrow \quad h^{2}+k^{2}+g h+f k+\frac{c}{2}=0$
$\therefore$ Required equation of locus is
$$ x^{2}+y^{2}+g x+f y+\frac{c}{2}=0 $$
