Circle 3 Question 4
4. The straight line $x+2 y=1$ meets the coordinate axes at $A$ and $B$. A circle is drawn through $A, B$ and the origin. Then, the sum of perpendicular distances from $A$ and $B$ on the tangent to the circle at the origin is
(2019 Main, 11 Jan I)
(a) $2 \sqrt{5}$
(b) $\frac{\sqrt{5}}{4}$
(c) $4 \sqrt{5}$
(d) $\frac{\sqrt{5}}{2}$
Show Answer
Answer:
Correct Answer: 4. (d)
Solution:
- According to given information, we have the following figure.
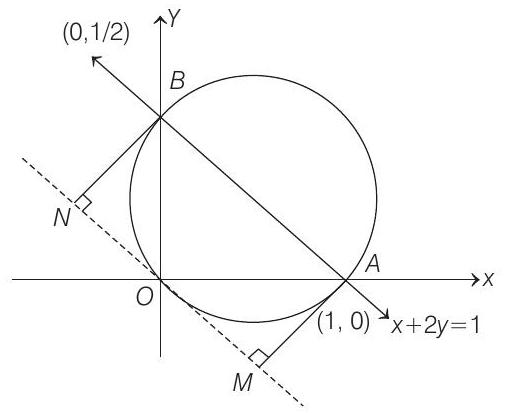
From figure, equation of circle (diameter form) is $(x-1)(x-0)+(y-0) y-\frac{1}{2}=0$
$$ \Rightarrow \quad x^{2}+y^{2}-x-\frac{y}{2}=0 $$
Equation of tangent at $(0,0)$ is $x+\frac{y}{2}=0$
$\left[\because\right.$ equation of tangent at $\left(x _1, y _1\right)$ is given by $T=0$.
Here, $T=0$
$$ \begin{array}{ll} \left.\Rightarrow x x _1+y y _1-\frac{1}{2}\left(x+x _1\right)-\frac{1}{4}\left(y+y _1\right)=0\right] \\ \Rightarrow & 2 x+y=0 \end{array} $$
Now, $\quad A M=\frac{|2 \cdot 1+1 \cdot 0|}{\sqrt{5}}=\frac{2}{\sqrt{5}}$
$\left[\because\right.$ distance of a point $P\left(x _1, y _1\right)$ from a line
$$ \begin{aligned} & \text { and } \quad B N=\frac{\left.\mid 2 \cdot b y+c=0 \text { is } \frac{\left|a x _1+b y _1+c\right|}{\sqrt{a^{2}+b^{2}}}\right]}{\sqrt{5} \frac{1}{2} \mid}=\frac{1}{2 \sqrt{5}} \\ & \therefore A M+B N=\frac{2}{\sqrt{5}}+\frac{1}{2 \sqrt{5}}=\frac{4+1}{2 \sqrt{5}}=\frac{\sqrt{5}}{2} \end{aligned} $$
