Circle 3 Question 3
3. The tangent and the normal lines at the point $(\sqrt{3}, 1)$ to the circle $x^{2}+y^{2}=4$ and the $X$-axis form a triangle. The area of this triangle (in square units) is
(a) $\frac{1}{3}$
(b) $\frac{4}{\sqrt{3}}$
(c) $\frac{2}{\sqrt{3}}$
(d) $\frac{1}{\sqrt{3}}$
(2019 Main, 8 April II)
Show Answer
Answer:
Correct Answer: 3. (c)
Solution:
- Let $T=0$ and $N=0$ represents the tangent and normal lines at the point $P(\sqrt{3}, 1)$ to the circle $x^{2}+y^{2}=4$.
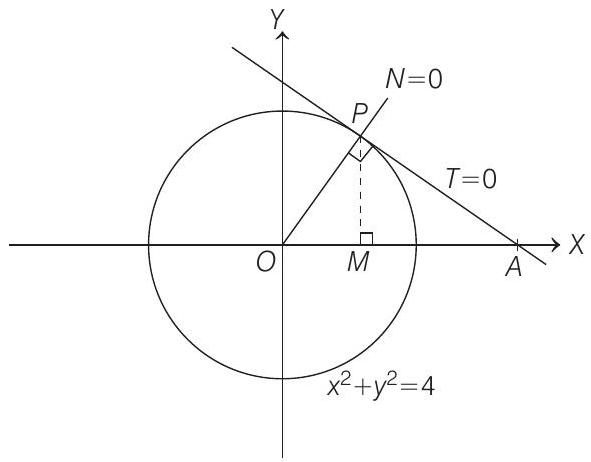
So, equation of tangent $(T=0)$ is
$$ \sqrt{3} x+y=4 $$
For point $A$, put $y=0$, we get
$$ x=\frac{4}{\sqrt{3}} $$
$\because$ Area of required $\triangle O P A=\frac{1}{2}(O A)(P M)$
$$ \begin{aligned} & =\frac{1}{2} \times \frac{4}{\sqrt{3}} \times 1 \\ & \quad[\because P M=y \text {-coordinate of } P] \\ & =\frac{2}{\sqrt{3}} \text { sq unit } \end{aligned} $$
