Circle 3 Question 10
10. Let $R S$ be the diameter of the circle $x^{2}+y^{2}=1$, where $S$ is the point $(1,0)$. Let $P$ be a variable point (other than $R$ and $S$ ) on the circle and tangents to the circle at $S$ and $P$ meet at the point $Q$. The normal to the circle at $P$ intersects a line drawn through $Q$ parallel to $R S$ at point $E$. Then, the locus of $E$ passes through the point(s)
(a) $\frac{1}{3}, \frac{1}{\sqrt{3}}$
(b) $\frac{1}{4}, \frac{1}{2}$
(c) $\frac{1}{3},-\frac{1}{\sqrt{3}}$
(d) $\frac{1}{4},-\frac{1}{2}$
(2016 Adv.)
Show Answer
Answer:
Correct Answer: 10. $(a, c)$
Solution:
- Given, $R S$ is the diameter of $x^{2}+y^{2}=1$.
Here, equation of the tangent at $P(\cos \theta, \sin \theta)$ is $x \cos \theta+y \sin \theta=1$.
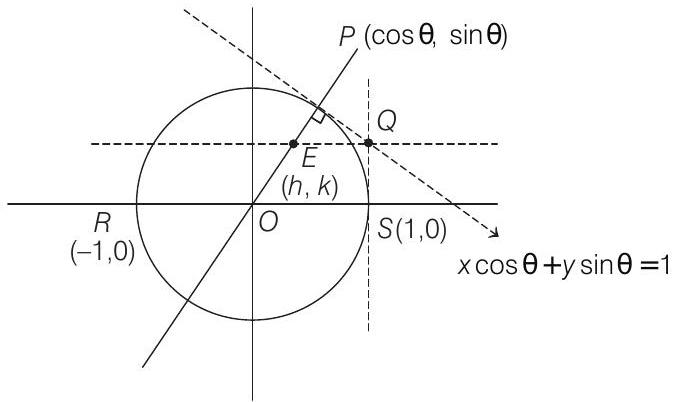
Intersecting with $x=1$,
$$ \begin{aligned} & y=\frac{1-\cos \theta}{\sin \theta} \\ \therefore \quad & Q 1, \frac{1-\cos \theta}{\sin \theta} \end{aligned} $$
$\therefore \quad$ Equation of the line through $Q$ parallel to $R S$ is
$$ y=\frac{1-\cos \theta}{\sin \theta}=\frac{2 \sin ^{2} \frac{\theta}{2}}{2 \sin \frac{\theta}{2} \cos \frac{\theta}{2}}=\tan \frac{\theta}{2} . $$
Normal at $P: y=\frac{\sin \theta}{\cos \theta} \cdot x$
$$ \Rightarrow \quad y=x \tan \theta $$
Let their point of intersection be $(h, k)$.
$$ \begin{aligned} & \text { Then, } \quad k=\tan \frac{\theta}{2} \text { and } k=h \tan \theta \\ & \therefore \quad k=h \frac{2 \tan \frac{\theta}{2}}{1-\tan ^{2} \frac{\theta}{2}} \Rightarrow k=\frac{2 h \cdot k}{1-k^{2}} \end{aligned} $$
$\Rightarrow \quad k\left(1-k^{2}\right)=2 h k$
$\therefore$ Locus for point $E: 2 x=\left(1-y^{2}\right)$
When $x=\frac{1}{3}$, then
$$ 1-y^{2}=\frac{2}{3} \Rightarrow y^{2}=1-\frac{2}{3} \Rightarrow y= \pm \frac{1}{\sqrt{3}} $$
$\therefore \frac{1}{3}, \pm \frac{1}{\sqrt{3}}$ satisfy $2 x=1-y^{2}$.
When $x=\frac{1}{4}$, then
$$ 1-y^{2}=\frac{2}{4} \Rightarrow y^{2}=1-\frac{1}{2} \Rightarrow y= \pm \frac{1}{\sqrt{2}} $$
$\therefore \quad \frac{1}{4}, \pm \frac{1}{2}$ does not satisfy $1-y^{2}=2 x$.
