Circle 2 Question 5
6. If one of the diameters of the circle, given by the equation,
(a)
(b)
(c) 5
(d) 10
(2016 Main)
Show Answer
Answer:
Correct Answer: 6. (c)
Solution:
- Given equation of a circle is
Now, according to given information, we have the following figure.
Clearly,
Now, in
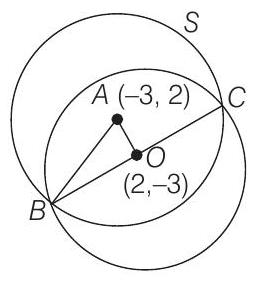
and






