Circle 2 Question 21
22. Let
Show Answer
Solution:
- Let the given circles
Let the variable circle
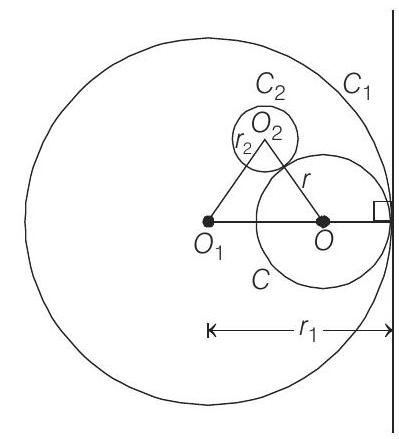
Now,
which is greater than
Alternate Solution
Let equations of
Let cetnre
Required locus is
which represents an ellipse whose foci are






