Circle 2 Question 19
20. A line
(a)
(b)
(c) 1 sq unit
(d) 2 sq units
Match the Columns
Show Answer
Solution:
- Since,
As,
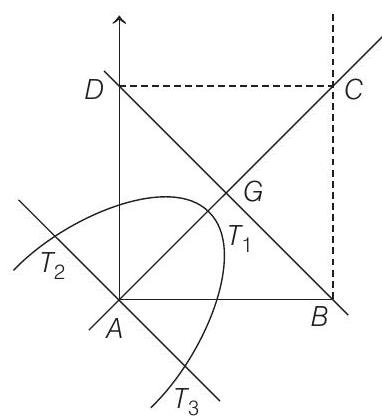
Also,






