Circle 1 Question 7
7. The centre of circle inscribed in square formed by the lines $x^{2}-8 x+12=0$ and $y^{2}-14 y+45=0$, is $(2003,1 M)$
(a) $(4,7)$
(b) $(7,4)$
(c) $(9,4)$
(d) $(4,9)$
Show Answer
Answer:
Correct Answer: 7. (c)
Solution:
- Given, circle is inscribed in square formed by the lines $x^{2}-8 x+12=0$ and $y^{2}-14 y+45=0$
$\Rightarrow \quad x=6 \quad$ and $x=2, y=5$ and $y=9$
which could be plotted as
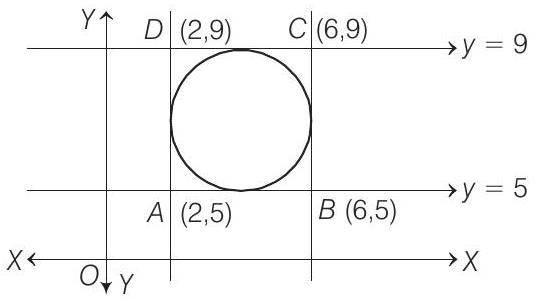
where, $A B C D$ clearly forms a square.
$\therefore$ Centre of inscribed circle
$=$ Point of intersection of diagonals
$=$ Mid-point of $A C$ or $B D$
$$ =\frac{2+6}{2}, \frac{5+9}{2}=(4,7) $$
$\Rightarrow$ Centre of inscribed circle is $(4,7)$.
