Circle 1 Question 5
5. If the area of an equilateral triangle inscribed in the circle, $x^{2}+y^{2}+10 x+12 y+c=0$ is $27 \sqrt{3}$ sq units, then $c$ is equal to
(2019 Main, 10 Jan II)
(a) 20
(b) -25
(c) 13
(d) 25
Show Answer
Answer:
Correct Answer: 5. (c)
Solution:
- Clearly, centre of the circumscribed circle is the centroid $(G)$ of the equilateral triangle $A B C$.
$[\because$ in an equilateral triangle circumcentre and centroid coincide]
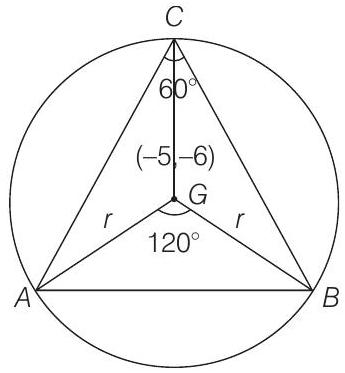
Also, we know that
$\triangle A G B \cong \triangle B G C \cong \triangle C G A$ [by SAS congruence rule]
$\therefore \quad \operatorname{ar}(\triangle A B C)=3 \operatorname{ar}(\triangle A G B)$
$$ \begin{aligned} =3 & \frac{1}{2} r^{2} \sin 120^{\circ} \\ & \quad\left[\because \text { area of triangle }=\frac{1}{2} a b \sin (\angle C)\right] \end{aligned} $$
$\because \quad \operatorname{ar}(\triangle A B C)=27 \sqrt{3}$
[given]
$\therefore \quad \frac{3}{2} r^{2} \frac{\sqrt{3}}{2}=27 \sqrt{3}$
$\left[\sin 120^{\circ}=\sin \left(180^{\circ}-60^{\circ}\right)=\sin 60^{\circ}=\frac{\sqrt{3}}{2}\right]$
$$ \Rightarrow \quad r^{2}=4 \times 9 $$
$\Rightarrow \quad r=6$
Now, radius of circle,
$$ \begin{aligned} r & =\sqrt{g^{2}+f^{2}-c} \\ \Rightarrow \quad 6 & =\sqrt{25+36-c} \end{aligned} $$
[ $\because$ in the given equation of circle $2 g=10$ and $2 f=12 \Rightarrow g=5$ and $f=6$ ]
$$ \begin{array}{lc} \Rightarrow & 36=25+36-c \\ \Rightarrow & c=25 \end{array} $$
