Circle 1 Question 19
19. A circle passes through three points $A, B$ and $C$ with the line segment $A C$ as its diameter. $A$ line passing through $A$ intersects the chord $B C$ at a point $D$ inside the circle. If angles $D A B$ and $C A B$ are $\alpha$ and $\beta$ respectively and the distance between the point $A$ and the mid-point of the line segment $D C$ is $d$, prove that the area of the circle is
$$ \frac{\pi d^{2} \cos ^{2} \alpha}{\cos ^{2} \alpha+\cos ^{2} \beta+2 \cos \alpha \cos \beta \cos (\beta-\alpha)} $$
$(1996,5 M)$
Show Answer
Solution:
- Let the radius of the circle be $r$. Take $X$-axis along $A C$ and the $O(0,0)$ as centre of the circle. Therefore, coordinate of $A$ and $C$ are $(-r, 0)$ and $(r, 0)$, respectively.
Now, $\quad \angle B A C=\beta, \angle B O C=2 \beta$
Therefore, coordinates of $B$ are $(r \cos 2 \beta, r \sin 2 \beta)$.
And slope of $A D$ is $\tan (\beta-\alpha)$.
Let $(x, y)$ be the coordinates of the point $D$. Equation of $A D$ is
$$ y=\tan (\beta-\alpha)(x+r) $$
$[\because$ slope $=\tan (\beta-\alpha)$ and point is $(-r, 0)]$
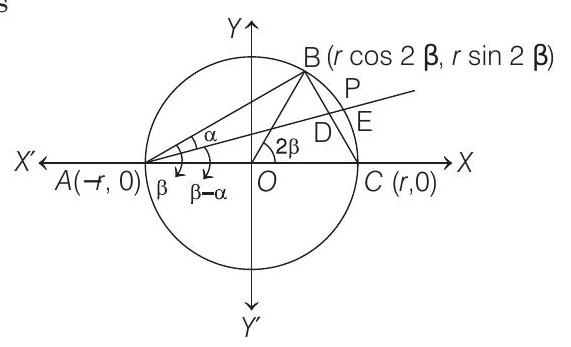
Now, equation of $B C$ is
$$ \begin{aligned} & & y=\frac{r \sin 2 \beta-0}{r \cos 2 \beta-r}(x-r) \\ \Rightarrow & y & =\frac{r \cdot 2 \sin \beta \cos \beta}{r\left(-2 \sin ^{2} \beta\right)}(x-r) \\ \Rightarrow & y & =\frac{2 \sin \beta \cos \beta}{-2 \sin ^{2} \beta}(x-r) \\ \Rightarrow & y & =-\cot \beta(x-r) \end{aligned} $$
To obtain the coordinate of $D$, solve Eqs. (i) and (ii) simultaneously
$$ \begin{array}{lc} \Rightarrow & \tan (\beta-\alpha)(x+r)=-\cot \beta(x-r) \\ \Rightarrow & x \tan (\beta-\alpha)+r \tan (\beta-\alpha)=-x \cot \beta+r \cot \beta \\ \Rightarrow \quad x[\tan (\beta-\alpha)+\cot \beta]=r[\cot \beta-\tan (\beta-\alpha)] \\ \Rightarrow \quad x \frac{\sin (\beta-\alpha)}{\cos (\beta-\alpha)}+\frac{\cos \beta}{\sin \beta}=r \frac{\cos \beta}{\sin \beta}-\frac{\sin (\beta-\alpha)}{\cos (\beta-\alpha)} \end{array} $$
$$ \begin{gathered} \Rightarrow \quad x \frac{\sin (\beta-\alpha) \sin \beta+\cos (\beta-\alpha) \cos \beta}{\cos (\beta-\alpha) \sin \beta} \\ =r \frac{\cos \beta \cos (\beta-\alpha)-\sin \beta \sin (\beta-\alpha)}{\sin \beta \cos (\beta-\alpha)} \\ \Rightarrow \quad x[\cos (\beta-\alpha-\beta)]=r[\cos (\beta-\alpha+\beta)] \\ \Rightarrow \quad x=\frac{r \cos (2 \beta-\alpha)}{\cos \alpha} \end{gathered} $$
On putting this value in Eq. (ii), we get
$$ \begin{aligned} y & =-\cot \beta \frac{r \cos (2 \beta-\alpha)}{\cos \alpha}-r \\ \Rightarrow \quad y & =-\frac{\cos \beta \cdot r}{\sin \beta} \frac{\cos (2 \beta-\alpha)-\cos \alpha}{\cos \alpha} \\ \Rightarrow \quad y & =-\frac{r \cos \beta}{\sin \beta} \frac{2 \sin \frac{2 \beta-\alpha+\alpha}{2} \sin \frac{\alpha-2 \beta+\alpha}{2}}{\cos \alpha} \\ \Rightarrow \quad y & =-\frac{r \cos \beta}{\sin \beta} \frac{2 \sin \beta \cdot \sin (\alpha-\beta)}{\cos \alpha} \\ & =-2 r \cos \beta \sin (\alpha-\beta) / \cos \alpha \end{aligned} $$
Therefore, coordinates of $D$ are
$$ \frac{r \cos (2 \beta-\alpha)}{\cos \alpha},-\frac{2 r \cos \beta \sin (\alpha-\beta)}{\cos \alpha} $$
Thus, coordinates of $E$ are
$$ \begin{aligned} & \frac{r \cos (2 \beta-\alpha)+r \cos \alpha}{2 \cos \alpha},-r \frac{\cos \beta \sin (\alpha-\beta)}{\cos \alpha} \\ & \Rightarrow \quad r \frac{2 \cos \frac{2 \beta-\alpha+\alpha}{2} \cdot \cos \frac{2 \beta-\alpha-\alpha}{2}}{2 \cos \alpha}, \\ & \Rightarrow \quad r \frac{\cos \beta \cdot \cos (\beta-\alpha)}{\cos \alpha}, r \frac{\cos \beta \sin (\beta-\alpha)}{\cos \alpha} \end{aligned} $$
Since, $A E=d$, we get
$$ \begin{aligned} & d^{2}=r^{2} \frac{\cos \beta \cos (\beta-\alpha)}{\cos \alpha}+1^{2}+r^{2} \frac{\cos \beta \sin (\beta-\alpha)}{\cos \alpha}{ }^{2} \\ & =\frac{r^{2}}{\cos ^{2} \alpha}\left[\cos ^{2} \beta \cos ^{2}(\beta-\alpha)+\cos ^{2} \alpha\right. \\ & \left.+2 \cos \beta \cos (\beta-\alpha) \cos \alpha+\cos ^{2} \beta \sin ^{2}(\beta-\alpha)\right] \\ & =\frac{r^{2}}{\cos ^{2} \alpha}\left[\cos ^{2} \beta{\cos ^{2}(\beta-\alpha)+\sin ^{2}(\beta-\alpha) }+\cos ^{2} \alpha\right. \\ & +2 \cos \beta \cos \alpha \cos (\beta-\alpha)] \\ & =\frac{r^{2}}{\cos ^{2} \alpha}\left[\cos ^{2} \beta+\cos ^{2} \alpha+2 \cos \alpha \cos \beta \cos (\beta-\alpha)\right] \\ & \Rightarrow r^{2}=\frac{d^{2} \cos ^{2} \alpha}{\cos ^{2} \beta+\cos ^{2} \alpha+2 \cos \alpha \cos \beta \cos (\beta-\alpha)} \end{aligned} $$
Therefore, area of the circle
$$ \pi r^{2}=\frac{\pi d^{2} \cos ^{2} \alpha}{\cos ^{2} \beta+\cos ^{2} \alpha+2 \cos \alpha \cos \beta \cos (\beta-\alpha)} $$
