Circle 1 Question 11
11. The centre of the circle passing through the point $(0,1)$ and touching the curve $y=x^{2}$ at $(2,4)$ is
(1983, 1M)
(a) $-\frac{16}{5}, \frac{27}{10}$
(b) $-\frac{16}{7}, \frac{53}{10}$
(c) $-\frac{16}{5}, \frac{53}{10}$
(d) None of the above
Objective Questions II
(One or more than one correct option)
Show Answer
Answer:
Correct Answer: 11. (a)
Solution:
- Let centre of circle be $(h, k)$. so that
$O A^{2}=O B^{2}$
$\Rightarrow \quad h^{2}+(k-1)^{2}=(h-2)^{2}+(k-4)^{2}$
$\Rightarrow \quad 4 h+6 k-19=0$
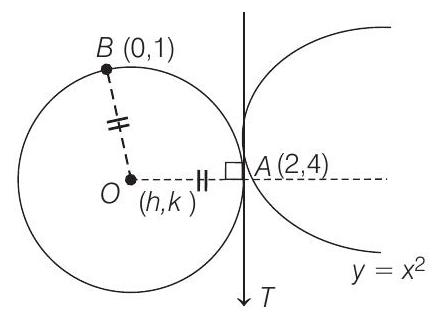
Also, slope of $O A=\frac{k-4}{h-2}$ and slope of tangent at $(2,4)$ to $y=x^{2}$ is 4.
and $($ slope of $O A) \cdot($ slope of tangent at $A)=-1$
$$ \begin{aligned} & \therefore \quad \frac{k-4}{h-2} \cdot 4=-1 \\ & \Rightarrow \quad 4 k-16=-h+2 \\ & h+4 k=18 \end{aligned} $$
On solving Eqs. (i) and (ii), we get
$$ k=\frac{53}{10} \text { and } h=-\frac{16}{5} $$
$\therefore$ Centre coordinates are $-\frac{16}{5}, \frac{53}{10}$.
