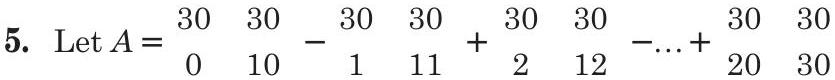Binomial Theorem 2 Question 4
4. For $r=0,1, \ldots, 10$, if $A _r, B _r$ and $C _r$ denote respectively the coefficient of $x^{r}$ in the expansions of $(1+x)^{10},(1+x)^{20}$ and $(1+x)^{30}$. Then, $\sum _{r=1}^{10} A _r\left(B _{10} B _r-C _{10} A _r\right)$ is equal to
(a) $B _{10}-C _{10}$
(b) $A _{10}\left(B _{10}^{2}-C _{10} A _{10}\right)$
(c) 0
(d) $C _{10}-B _{10}$
(2010)
Show Answer
Answer:
Correct Answer: 4. (d)
Solution:
- $A _r=$ Coefficient of $x^{r}$ in $(1+x)^{10}={ }^{10} C _r$
$B _r=$ Coefficient of $x^{r}$ in $(1+x)^{20}={ }^{20} C _r$
$C _r=$ Coefficient of $x^{r}$ in $(1+x)^{30}={ }^{30} C _r$
$\therefore \sum _{r=1}^{10} A _r\left(B _{10} B _r-C _{10} A _r\right)=\sum _{r=1}^{10} A _r B _{10} B _r-\sum _{r=1}^{10} A _r C _{10} A _r$
$=\sum _{r=1}^{10}{ }^{10} C _r{ }^{20} C _{10}{ }^{20} C _r-\sum _{r=1}^{10}{ }^{10} C _r{ }^{30} C _{10}{ }^{10} C _r$
$=\sum _{r=1}^{10}{ }^{10} C _{10-r}{ }^{20} C _{10}{ }^{20} C _r-\sum _{r=1}^{10}{ }^{10} C _{10-r}{ }^{30} C _{10}{ }^{10} C _r$
$={ }^{20} C _{10} \sum _{r=1}^{10}{ }^{10} C _{10-r} \cdot{ }^{20} C _r-{ }^{30} C _{10} \sum _{r=1}^{10}{ }^{10} C _{10-r}{ }^{10} C _r$
$={ }^{20} C _{10}\left({ }^{30} C _{10}-1\right)-{ }^{30} C _{10}\left({ }^{20} C _{10}-1\right)$
$={ }^{30} C _{10}-{ }^{20} C _{10}=C _{10}-B _{10}$
$\therefore \quad A={ }^{30} C _0{ }^{30} C _{10}-{ }^{30} C _1{ }^{30} C _{11}+{ }^{30} C _2{ }^{30} C _{12}$
$=$ Coefficient of $x^{20}$ in $(1+x)^{30}(1-x)^{30}$
$-\ldots+{ }^{30} C _{20}{ }^{30} C _{30}$
$=$ Coefficient of $x^{20}$ in $\left(1-x^{2}\right)^{30}$
$=$ Coefficient of $x^{20}$ in $\sum _{r=0}^{30}(-1)^{r^{30}} C _r\left(x^{2}\right)^{r}$
$=(-1)^{10}{ }^{30} C _{10} \quad$ [for coefficient of $x^{20}$, put $r=10$ ] $={ }^{30} C _{10}$
