Binomial Theorem 1 Question 4
5. If some three consecutive coefficients in the binomial expansion of $(x+1)^{n}$ in powers of $x$ are in the ratio $2: 15$ : 70 , then the average of these three coefficients is
(2019 Main, 9 April II)
(a) 964
(b) 227
(c) 232
(d) 625
Show Answer
Answer:
Correct Answer: 5. (d)
Solution:
Key Idea Use general term of Binomial expansion $(x+a)^{n}$ i.e.
$T _{r+1}={ }^{n} C _{r 1} x^{n-r} a^{r}$
Given binomial is $(x+1)^{n}$, whose general term, is $T _{r+1}={ }^{n} C _r x^{r}$
According to the question, we have
${ }^{n} C _{r-1}:{ }^{n} C _r:{ }^{n} C _{r+1}=2: 15: 70$
Now, $\quad \frac{{ }^{n} C _{r-1}}{{ }^{n} C _r}=\frac{2}{15}$
$\Rightarrow \quad \frac{\frac{n !}{(r-1) !(n-r+1) !}}{\frac{n !}{r !(n-r) !}}=\frac{2}{15}$ $\Rightarrow \quad \frac{r}{n-r+1}=\frac{2}{15} \Rightarrow 15 r=2 n-2 r+2$ $\Rightarrow \quad 2 n-17 r+2=0$
$\Rightarrow \quad \frac{r+1}{n-r}=\frac{3}{14} \Rightarrow 14 r+14=3 n-3 r$
$\Rightarrow \quad 3 n-17 r-14=0$
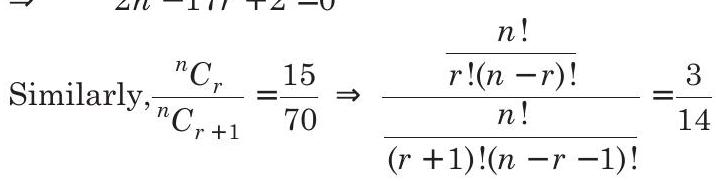
On solving Eqs. (i) and (ii), we get
$n-16=0 \Rightarrow n=16$ and $r=2$
Now, the average $=\frac{{ }^{16} C _1+{ }^{16} C _2+{ }^{16} C _3}{3}$
$$ =\frac{16+120+560}{3}=\frac{696}{3}=232 $$
