Binomial Theorem 1 Question 33
35. Given,
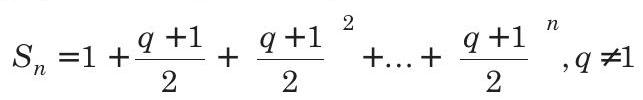
Prove that
Integer Answer Type Question
Show Answer
Solution:
where
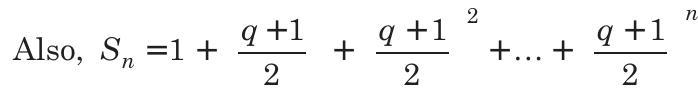
From Eqs. (i) and (ii),
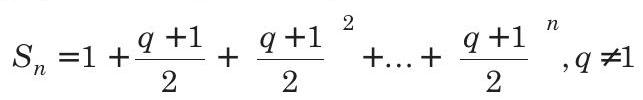
Prove that
where
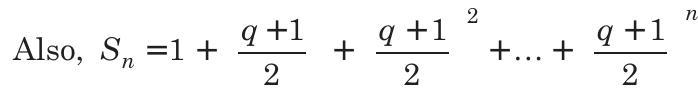
From Eqs. (i) and (ii),
Welcome to SATHEE !
Select from 'Menu' to explore our services, or ask SATHEE to get started. Let's embark on this journey of growth together! 🌐📚🚀🎓
I'm relatively new and can sometimes make mistakes.
If you notice any error, such as an incorrect solution, please use the thumbs down icon to aid my learning.
To begin your journey now, click on "I understand".
