Binomial Theorem 1 Question 18
19. Coefficient of
(2014 Adv.)
(a) 1051
(b) 1106
(c) 1113
(d) 1120
Show Answer
Answer:
Correct Answer: 19.
Solution:
- Coefficient of
In this type of questions, we find different composition of terms where product will give us
Now, consider the following cases for
Coefficient of
Coefficient of
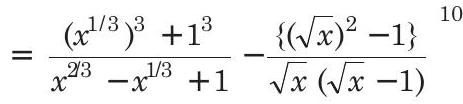
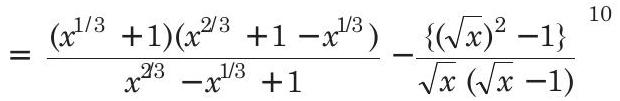
For independent of






