Application of Derivatives 4 Question 7
8. The maximum area (in sq. units) of a rectangle having its base on the $X$-axis and its other two vertices on the parabola, $y=12-x^{2}$ such that the rectangle lies inside the parabola, is
(2019 Main, 12 Jan I)
(a) 36
(b) $20 \sqrt{2}$
(c) 32
(d) $18 \sqrt{3}$
Show Answer
Answer:
Correct Answer: 8. (c)
Solution:
- Equation of parabola is given, $y=12-x^{2}$
or $\quad x^{2}=-(y-12)$.
Note that vertex of parabola is $(0,12)$ and its open downward.
Let $Q$ be one of the vertices of rectangle which lies on parabola. Then, the coordinates of $Q$ be $\left(a, 12-a^{2}\right)$
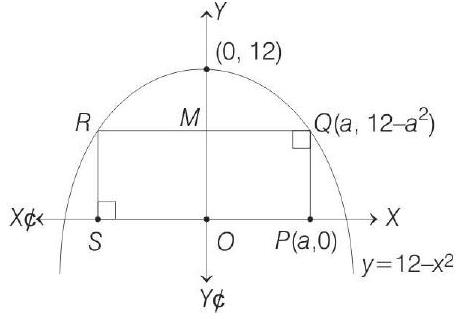
Then, area of rectangle $P Q R S$
$=2 \times($ Area of rectangle $P Q M O)$
[due to symmetry about $Y$-axis]
$$ =2 \times\left[a\left(12-a^{2}\right)\right]=24 a-2 a^{3}=\Delta(\text { let }) . $$
The area function $\Delta _d$ will be maximum, when
$$ \begin{array}{cc} & \frac{d \Delta}{d a}=0 \\ \Rightarrow \quad 24-6 a^{2}=0 \\ \Rightarrow \quad a^{2}=4 \Rightarrow a=2 \\ \text { So, maximum area of rectangle } & \\ \text { PQRS }=(24 \times 2)-2(2)^{3} \\ & =48-16=32 \text { sq units } \end{array} $$
