Application of Derivatives 4 Question 5
6. If $S _1$ and $S _2$ are respectively the sets of local minimum and local maximum points of the function, $f(x)=9 x^{4}+12 x^{3}-36 x^{2}+25, x \in R$, then
(a) $S _1={-2} ; S _2={0,1}$
(2019 Main, 8 April I)
(b) $S _1={-2,0} ; S _2={1}$
(c) $S _1={-2,1} ; S _2={0}$
(d) $S _1={-1} ; S _2={0,2}$
Show Answer
Answer:
Correct Answer: 6. (c)
Solution:
- Given function is
$f(x)=9 x^{4}+12 x^{3}-36 x^{2}+25=y$ (let)
For maxima or minima put $\frac{d y}{d x}=0$
$\Rightarrow \quad \frac{d y}{d x}=36 x^{3}+36 x^{2}-72 x=0$
$\Rightarrow \quad x^{3}+x^{2}-2 x=0$
$\Rightarrow \quad x\left[x^{2}+x-2\right]=0$
$\Rightarrow \quad x\left[x^{2}+2 x-x-2\right]=0$
$\Rightarrow \quad x[x(x+2)-1(x+2)]=0$
$\Rightarrow \quad x(x-1)(x+2)=0$
$\Rightarrow \quad x=-2,0,1$
By sign method, we have following
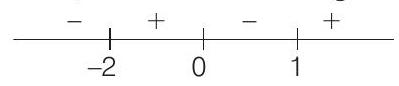
Since, $\frac{d y}{d x}$ changes it’s sign from negative to positive at $x=$ ’ 2 ’ and ’ 1 ‘, so $x=-2,1$ are points of local minima. Also, $\frac{d y}{d x}$ changes it’s sign from positive to negative at $x=0$, so $x=0$ is point of local maxima.
$\therefore S _1={-2,1}$ and $S _2={0}$.
