Application of Derivatives 4 Question 49
52. What normal to the curve $y=x^{2}$ forms the shortest chord?
(1992, 6M)
Show Answer
Answer:
Correct Answer: 52. $x=0, y=0$ 59. $\frac{u d}{\sqrt{v^{2}-u^{2}}}$
Solution:
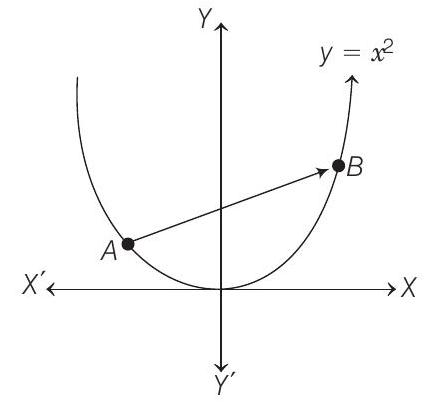
Any point on the parabola $y=x^{2}$ is of the form $\left(t, t^{2}\right)$.
Now, $\quad \frac{d y}{d x}=2 x \quad \Rightarrow \quad \frac{d y}{d x}{ } _{x=t}=2 t$
Which is the slope of the tangent. So, the slope of the normal to $y=x^{2}$ at $A\left(t, t^{2}\right)$ is $-1 / 2 t$.
Therefore, the equation of the normal to
$$ \begin{aligned} y & =x^{2} \text { at } A\left(t, t^{2}\right) \text { is } \\ y-t^{2} & =-\frac{1}{2 t} \quad(x-t) \end{aligned} $$
Suppose Eq. (i) meets the curve again at $B\left(t _1, t _1^{2}\right)$. Then, $\quad t _1^{2}-t^{2}=-\frac{1}{2 t}\left(t _1-t\right)$
$\Rightarrow \quad\left(t _1-t\right)\left(t _1+t\right)=-\frac{1}{2 t}\left(t _1-t\right)$
$\Rightarrow \quad\left(t _1+t\right)=-\frac{1}{2 t}$
$\Rightarrow \quad t _1=-t-\frac{1}{2 t}$
Therefore, length of chord,
$$ \begin{aligned} L & =A B^{2}=\left(t-t _1\right)^{2}+\left(t^{2}-t _1^{2}\right)^{2} \\ & =\left(t-t _1\right)^{2}+\left(t-t _1\right)^{2}\left(t+t _1\right)^{2} \\ & =\left(t-t _1\right)^{2}\left[1+\left(t+t _1\right)^{2}\right] \\ & =t+t+\frac{1}{2 t}^{2} 1+t-t-\frac{1}{2 t}^{2} \\ \Rightarrow \quad L & =2 t+\frac{1}{2 t}^{2} 1+\frac{1}{4 t^{2}}=4 t^{2} 1+{\frac{1}{4 t^{2}}}^{3} \end{aligned} $$
On differentiating w.r.t. $t$, we get
$$ \begin{aligned} \frac{d L}{d t} & =8 t \quad 1+{\frac{1}{4 t^{2}}}^{3}+12 t^{2} \quad 1+{\frac{1}{4 t^{2}}}^{2}-\frac{2}{4 t^{3}} \\ & =2 \quad 1+{\frac{1}{4 t^{2}}}^{2} \quad 4 t \quad 1+\frac{1}{4 t^{2}} \quad-\frac{3}{t} \\ & =2 \quad 1+{\frac{1}{4 t^{2}}}^{2} \quad 4 t-\frac{2}{t}=4 \quad 1+{\frac{1}{4 t^{2}}} _2^{2} \quad 2 t-\frac{1}{t} \end{aligned} $$
For maxima or minima, we must have $\frac{d L}{d t}=0$
$$ \begin{aligned} \Rightarrow & & 2 t-\frac{1}{t} & =0 \Rightarrow \\ \Rightarrow & & t & = \pm \frac{1}{\sqrt{2}} \end{aligned} $$
Now, $\frac{d^{2} L}{d t^{2}}=8 \quad 1+\frac{1}{4 t^{2}} \quad-\frac{1}{2 t^{3}} \quad 2 t-\frac{1}{t}$
$$ \Rightarrow \quad \frac{d^{2} L}{d t^{2}}{ } _{t= \pm 1 / \sqrt{2}}=0+4 \quad 1+{\frac{1}{4 t^{2}}}^{2} 2+\frac{1}{t^{2}} $$
Therefore, $L$ is minimum, when $t= \pm 1 / \sqrt{2}$. For $t=1 / \sqrt{2}$, point $A$ is $(1 / \sqrt{2}, 1 / 2)$ and point $B$ is $(-\sqrt{2}, 2)$. When $t=-1 / \sqrt{2}, A$ is $(-1 / \sqrt{2}, 1 / 2), B$ is $(\sqrt{2}, 2)$.
Again, when $t=1 / \sqrt{2}$, the equation of $A B$ is
$$ \begin{aligned} \frac{y-2}{\frac{1}{2}-2} & =\frac{x+\sqrt{2}}{\frac{1}{\sqrt{2}}+\sqrt{2}} \\ \Rightarrow \quad(y-2) \quad \frac{1}{\sqrt{2}}+\sqrt{2} & =\left(x+\sqrt{2)} \quad \frac{1}{2}-2\right. \\ \Rightarrow \quad \sqrt{2} x+2 y-2 & =0 \end{aligned} $$
and when $t=-1 / \sqrt{2}$, the equation of $A B$ is
$$ \begin{aligned} \frac{y-2}{\frac{1}{2}-2} & =\frac{x-\sqrt{2}}{-\frac{1}{\sqrt{2}}-\sqrt{2}} \\ \Rightarrow \quad(y-2)-\frac{1}{\sqrt{2}}-\sqrt{2} & =(x-\sqrt{2}) \frac{1}{2}-2 \\ \Rightarrow \sqrt{2} x-2 y+2 & =0 \end{aligned} $$
