SATHEE: Application of Derivatives 4 Question 45

Application of Derivatives 4 Question 45

47. If $S$ is a square of unit area. Consider any quadrilateral which has one vertex on each side of $S$ . If $a, b, c$ and $d$ denote the length of the sides of the quadrilateral, then prove that $2 \leq a^{2} + b^{2} + d^{2} \leq 4$ .

$(1997, 5$ M)

Show Answer

Answer:

Correct Answer: 47. $\sqrt{2} x - 2 y + 2 = 0, \sqrt{2} x + 2 y - 2 = 0$

Solution:

Let the square $S$ is to be bounded by the lines $x = \pm 1 / 2$ and $y = \pm 1 / 2$ .

We have, $a^{2} = x_{1} - {\frac{1}{2}}^{2} + \frac{1}{2} - y_{1}^{2}$

$= x_{1}^{2} - y_{1}^{2} - x_{1} - y_{1} + \frac{1}{2}$

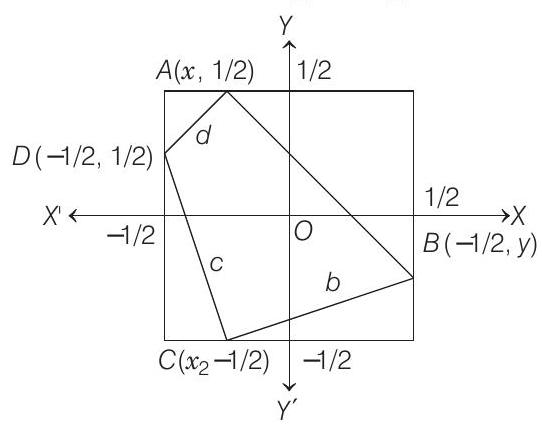
Similarly, $b^{2} = x_{2}^{2} - y_{1}^{2} - x_{2} + y_{1} + \frac{1}{2}$

$c^{2} = x_{2}^{2} - y_{2}^{2} + x_{2} + y_{2} + \frac{1}{2}$

$d^{2} = x_{1}^{2} - y_{2}^{2} + x_{1} - y_{2} + \frac{1}{2}$

$∴ a^{2} + b^{2} + c^{2} + d^{2} = 2 (x_{1}^{2} + y_{1}^{2} + x_{2}^{2} + y_{2}^{2}) + 2$

Therefore, $0 \leq x_{1}^{2}, x_{2}^{2}, y_{1}^{2}, y_{2}^{2} \leq \frac{1}{4}$

$\begin{array}{lc} 0 \leq x_{1}^{2} + x_{2}^{2} + y_{1}^{2} + y_{2}^{2} \leq 1 \\ \Rightarrow & 0 \leq 2 (x_{1}^{2} + x_{2}^{2} + y_{1}^{2} + y_{2}^{2}) \leq 2 \\ But & 2 \leq 2 (x_{1}^{2} + x_{2}^{2} + y_{1}^{2} + y_{2}^{2}) + 2 \leq 4 \end{array}$

Alternate Solution

$c^{2} = x_{2}^{2} + y_{2}^{2}$

$\begin{aligned} b^{2} & = {(1 - x_{2})}^{2} + y_{1}^{2} \\ a^{2} & = {(1 - y_{1})}^{2} + {(1 - x_{1})}^{2} \\ d^{2} & = x_{1}^{2} + {(1 - y_{2})}^{2} \end{aligned}$

On adding Eqs. (i), (ii), (iii) and (iv), we get

$a^{2} + b^{2} + c^{2} + d^{2} = x_{1}^{2} + {(1 - x_{1})}^{2} + y_{1}^{2} + {(1 - y_{1})}^{2}$

$+ x_{2}^{2} + {(1 - x_{2})}^{2} + y_{2}^{2} + {(1 - y_{2})}^{2}$

where $x_{1}, y_{1}, x_{2}, y_{2}$ all vary in the interval $[0, 1]$ .

Now, consider the function $y = x^{2} + (1 - x)^{2}, 0 \leq x \leq 1$ differentiating $\Rightarrow \frac{d y}{d x} = 2 x - 2 (1 - x)$ . For maximum or $minimum \frac{d y}{d x} = 0$ .

$\Rightarrow 2 x - 2 (1 - x) = 0 \Rightarrow 2 x - 2 + 2 x = 0$

$\Rightarrow 4 x = 2 \Rightarrow x = 1 / 2$

Again

$\frac{d^{2} y}{d x^{2}} = 2 + 2 = 4$

Hence, $y$ is minimum at $x = \frac{1}{2}$ and its minimum value is $1 / 4$ . Clearly, value is maximum when $x = 1$ .

$∴$ Minimum value of $a^{2} + b^{2} + c^{2} + d^{2} = \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} = 2$ and maximum value is $1 + 1 + 1 + 1 = 4$