SATHEE: Application of Derivatives 4 Question 41

Application of Derivatives 4 Question 41

43. For the circle $x^{2} + y^{2} = r^{2}$ , find the value of $r$ for which the area enclosed by the tangents drawn from the point $P (6, 8)$ to the circle and the chord of contact is maximum.

(2003, 2M)

Show Answer

Answer:

Correct Answer: 43. Maxima at $x = \frac{(b - \sqrt{b^{2} - 1})}{4}$ and minima at $x = \frac{1}{4} (b + \sqrt{b^{2} - 1})$

Solution:

To maximise area of $△ A P B$ , we know that, $O P = 10$ and $\sin θ = r / 10$ , where $θ \in (0, π / 2)$

$∴$ Area $= \frac{1}{2} (2 A Q) (P Q)$

$\begin{aligned} = A Q \cdot P Q = (r \cos θ) (10 - O Q) \\ = (r \cos θ) (10 - r \sin θ) \\ = 10 \sin θ \cos θ (10 - 10 \sin^{2} θ) [from Eq. (i)] \end{aligned}$

$\Rightarrow A = 100 \cos^{3} θ \sin θ$

$\Rightarrow \frac{d A}{d θ} = 100 \cos^{4} θ - 300 \cos^{2} θ \cdot \sin^{2} θ$

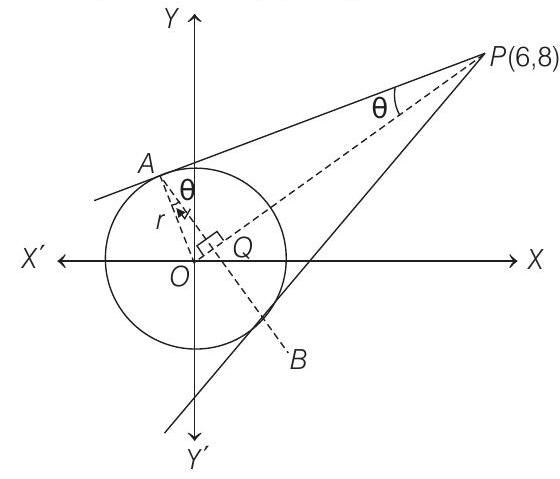
Put $\frac{d A}{d θ} = 0$

$\Rightarrow \cos^{2} θ = 3 \sin^{2} θ$

$\Rightarrow \tan θ = 1 / \sqrt{3}$

$\Rightarrow θ = π / 6$

At which $\frac{d A}{d θ} < 0$ , thus when $θ = π / 6$ , area is maximum

From Eq. (i), $r = 10 \sin \frac{π}{6} = 5$ units

पिछला

अगला

Application of Derivatives 4 Question 41

43. For the circle $x^{2} + y^{2} = r^{2}$ , find the value of $r$ for which the area enclosed by the tangents drawn from the point $P (6, 8)$ to the circle and the chord of contact is maximum.

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Application of Derivatives 4 Question 41

43. For the circle x2+y2=r2, find the value of r for which the area enclosed by the tangents drawn from the point P(6,8) to the circle and the chord of contact is maximum.

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

43. For the circle $x^{2} + y^{2} = r^{2}$ , find the value of $r$ for which the area enclosed by the tangents drawn from the point $P (6, 8)$ to the circle and the chord of contact is maximum.