Application of Derivatives 4 Question 4
4. If $f(x)$ is a non-zero polynomial of degree four, having local extreme points at $x=-1,0,1$, then the set $S={x \in R: f(x)=f(0)}$ contains exactly
(a) four rational numbers
(2019 Main, 9 April I)
(b) two irrational and two rational numbers
(c) four irrational numbers
(d) two irrational and one rational number
Show Answer
Answer:
Correct Answer: 4. (d)
Solution:
- The non-zero four degree polynomial $f(x)$ has extremum points at $x=-1,0,1$, so we can assume $f^{\prime}(x)=a(x+1)(x-0)(x-1)=a x\left(x^{2}-1\right)$
where, $a$ is non-zero constant.
$$ f^{\prime}(x)=a x^{3}-a x $$
$\Rightarrow \quad f(x)=\frac{a}{4} x^{4}-\frac{a}{2} x^{2}+C$
[integrating both sides]
where, $C$ is constant of integration.
Now, since $f(x)=f(0)$
$\Rightarrow \frac{a}{4} x^{4}-\frac{a}{2} x^{2}+C=C \Rightarrow \frac{x^{4}}{4}=\frac{x^{2}}{2}$
$$ \Rightarrow \quad x^{2}\left(x^{2}-2\right)=0 \Rightarrow x=-\sqrt{2}, 0, \sqrt{2} $$
Thus, $f(x)=f(0)$ has one rational and two irrational roots.
Key Idea
(i) Use formula of volume of cylinder, $V=\pi r^{2} h$ where, $r=$ radius and $h=$ height
(ii) For maximum or minimum, put first derivative of $V$ equal to zero
Let a sphere of radius 3 , which inscribed a right circular cylinder having radius $r$ and height is $h$, so
From the figure, $\frac{h}{2}=3 \cos \theta$
$\Rightarrow \quad h=6 \cos \theta$
and
$r=3 \sin \theta$
$\because$ Volume of cylinder $V=\pi r^{2} h$ $=\pi(3 \sin \theta)^{2}(6 \cos \theta)=54 \pi \sin ^{2} \theta \cos \theta$. For maxima or minima, $\frac{d V}{d \theta}=0$
$\Rightarrow \quad 54 \pi\left[2 \sin \theta \cos ^{2} \theta-\sin ^{3} \theta\right]=0$
$\Rightarrow \quad \sin \theta\left[2 \cos ^{2} \theta-\sin ^{2} \theta\right]=0$
$\Rightarrow \quad \tan ^{2} \theta=2 \quad \because \theta \in 0, \frac{\pi}{2}$
$\Rightarrow \quad \tan \theta=\sqrt{2}$
$\Rightarrow \quad \sin \theta=\sqrt{\frac{2}{3}}$ and $\cos \theta=\frac{1}{\sqrt{3}}$
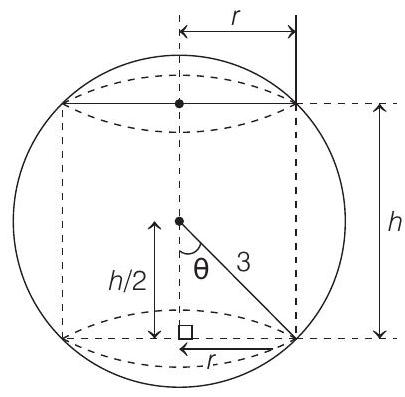
From Eqs. (i) and (ii), we get
$$ h=6 \frac{1}{\sqrt{3}}=2 \sqrt{3} $$
