Application of Derivatives 4 Question 34
36. The function
$f(x)=\int _{-1}^{x} t\left(e^{t}-1\right)(t-1)(t-2)^{3}(t-3)^{5} d t$ has a local minimum at $x$ equals
(1999, 3M)
(a) 0
(b) 1
(c) 2
(d) 3
Show Answer
Answer:
Correct Answer: 36. (a) $P \rightarrow 4 Q \rightarrow 1 R \rightarrow 2 S \rightarrow 3$
Solution:
- $f(x)=\int _{-1}^{x} t\left(e^{t}-1\right)(t-1)(t-2)^{3}(t-3)^{5} d t$
$$ \begin{gathered} f^{\prime}(x)=\frac{d}{d x} \int _{-1}^{x} t\left(e^{t}-1\right)(t-1)(t-2)^{3}(t-3)^{5} d t \\ =x\left(e^{x}-1\right)(x-1)(x-2)^{3}(x-3)^{5} \times 1 \\ \because \frac{d}{d x} \int _{\varphi(x)}^{\psi(x)} f(t) d t=f{\Psi(x)} \Psi^{\prime}(x)-f{\varphi(x)} \varphi^{\prime}(x) \end{gathered} $$
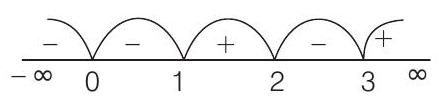
For local minimum, $f^{\prime}(x)=0$
$$ \Rightarrow \quad x=0,1,2,3 $$
Let $\quad f^{\prime}(x)=g(x)=x\left(e^{x}-1\right)(x-1)(x-2)^{3}(x-3)^{5}$
Using sign rule,
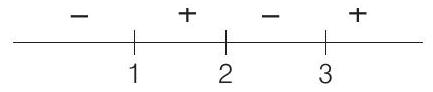
This shows that $f(x)$ has a local minimum at $x=1$ and $x=3$ and maximum at $x=2$.
Therefore, (b) and (d) are the correct answers.
