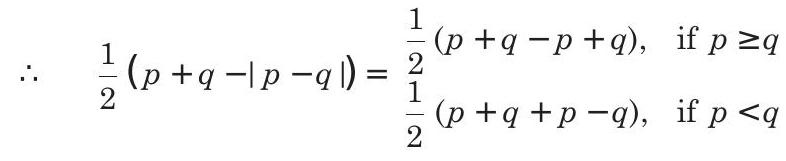Application of Derivatives 4 Question 28
29. If $p, q$ and $r$ are any real numbers, then
(a) $\max (p, q)<\max (p, q, r)$
$(1982,1 M)$
(b) $\min (p, q)=\frac{1}{2}(p+q-|p-q|)$
(c) $\max (p, q)<\min (p, q, r)$
(d) None of the above
Objective Questions II
(One or more than one correct option)
$$ \text { 30. If } f(x)=\begin{array}{ccc} \cos (2 x) & \cos (2 x) & \sin (2 x) \\ -\cos x & \cos x & -\sin x \text {, then } \\ \sin x & \sin x & \cos x \end{array} $$
(2017 Adv.) (a) $f(x)$ attains its minimum at $x=0$
(b) $f(x)$ attains its maximum at $x=0$
(c) $f^{\prime}(x)=0$ at more than three points in $(-\pi, \pi)$
(d) $f^{\prime}(x)=0$ at exactly three points in $(-\pi, \pi)$
Show Answer
Answer:
Correct Answer: 29. (a, b)
Solution:
- Since, $\max (p, q)=\begin{array}{ll}p, & \text { if } p>q\end{array}$
$$ q, \text { if } q>p $$
$p$, if $p$ is greatest.
and $\max (p, q, r)=q$, if $q$ is greatest.
$r$, if $r$ is greatest.
$\therefore \quad \max (p, q)<\max (p, q, r)$ is false.
We know that, $|p-q|=\begin{array}{ll}p-q, & \text { if } p \geq q \ q-p, & \text { if } p<q\end{array}$
$$ =\begin{array}{ll} q, & \text { if } p \geq q \\ p, & \text { if } p<q \end{array} $$
$\Rightarrow \quad \frac{1}{2}{p+q-|p-q|}=\min (p, q)$ $\cos 2 x \quad \cos 2 x \quad \sin 2 x$
