Application of Derivatives 4 Question 21
22. If $f(x)=\begin{aligned} & |x| \text {, for } 0<|x| \leq 2 \ & 1\end{aligned}$, for $\quad x=0$. Then, at $x=0, f$ has
(a) a local maximum
(b) no local maximum
(c) a local minimum
(d) no extremum
$(2000,1 M)$
Show Answer
Answer:
Correct Answer: 22. (b)
Solution:
- It is clear from figure that at $x=0, f(x)$ is not continuous.
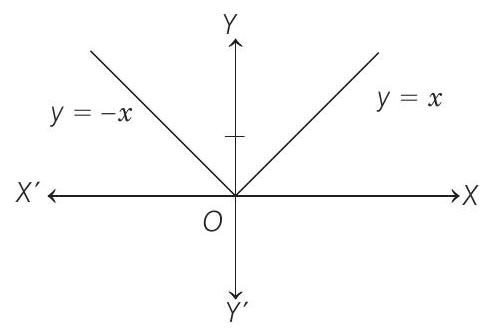
Here, $f(0)>$ RHL at $x=0$ and $f(0)>$ LHL at $x=0$
So, local maximum at $x=0$.
