Application of Derivatives 4 Question 17
18. The number of points in
(2013 Adv.)
(a) 6
(b) 4
(c) 2
(d) 0
Show Answer
Answer:
Correct Answer: 18. (c)
Solution:
- PLAN The given equation contains algebraic and trigonometric functions called transcendental equation. To solve transcendental equations we should always plot the graph for LHS and RHS.
Here,
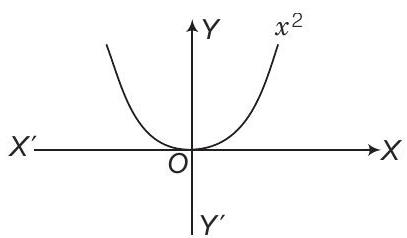
Let
We know that, the graph for
To plot,
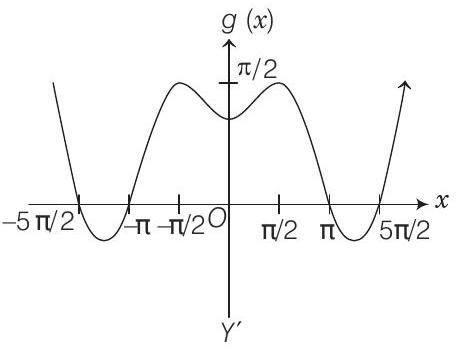
At
At
So, graph of
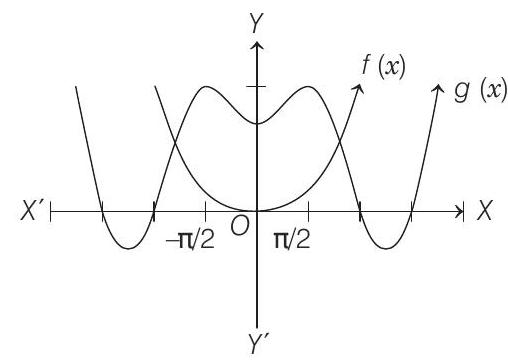
So, number of solutions are 2.






