Application of Derivatives 4 Question 12
13. If $20 m$ of wire is available for fencing off a flower-bed in the form of a circular sector, then the maximum area (in sq. m) of the flower-bed is
(2017 Main)
(a) 12.5
(b) 10
(c) 25
(d) 30
Show Answer
Answer:
Correct Answer: 13. (d)
Solution:
- Total length $=2 r+r \theta=20$
$$ \Rightarrow \quad \theta=\frac{20-2 r}{r} $$
Now, area of flower-bed,
$$ \begin{aligned} & A & =\frac{1}{2} r^{2} \theta \\ \Rightarrow \quad & A & =\frac{1}{2} r^{2} \frac{20-2 r}{r} \\ \Rightarrow \quad & A & =10 r-r^{2} \\ \therefore \quad & \frac{d A}{d r} & =10-2 r \end{aligned} $$
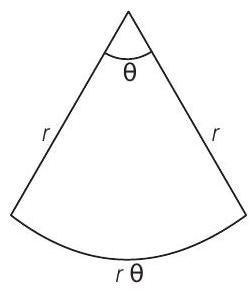
For maxima or minima, put $\frac{d A}{d r}=0$.
$$ \begin{aligned} \Rightarrow \quad 10-2 r & =0 \Rightarrow r=5 \\ \therefore \quad A _{\max } & =\frac{1}{2}(5)^{2} \frac{20-2(5)}{5} \\ & =\frac{1}{2} \times 25 \times 2=25 \text { sq. } m \end{aligned} $$
