Application of Derivatives 4 Question 10
11. The maximum volume (in cu.m) of the right circular cone having slant height $3 m$ is
(2019 Main, 9 Jan I)
(a) $\frac{4}{3} \pi$
(b) $2 \sqrt{3} \pi$
(c) $3 \sqrt{3} \pi$
(d) $6 \pi$
Show Answer
Answer:
Correct Answer: 11. (b)
Solution:
- Let $h$ =height of the cone,
$r=$ radius of circular base
$$ \begin{aligned} & =\sqrt{(3)^{2}-h^{2}} \quad\left[\because l^{2}=h^{2}+r^{2}\right] \\ & =\sqrt{9-h^{2}} \end{aligned} $$
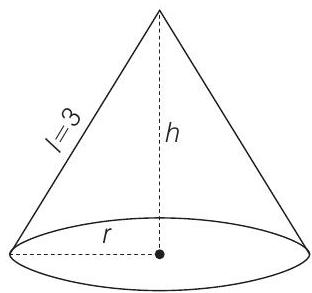
Now, volume $(V)$ of cone $=\frac{1}{3} \pi r^{2} h$
$$ \begin{aligned} \Rightarrow \quad V(h) & =\frac{1}{3} \pi\left(9-h^{2}\right) h \\ & =\frac{1}{3} \pi\left[9 h-h^{3}\right] \end{aligned} $$
For maximum volume $V^{\prime}(h)=0$ and $V^{\prime \prime}(h)<0$.
Here, $\quad V^{\prime}(h)=0 \Rightarrow\left(9-3 h^{2}\right)=0$
$$ \Rightarrow \quad h=\sqrt{3} $$
and $V^{\prime \prime}(h)=\frac{1}{3} \pi(-6 h)<0$ for $h=\sqrt{3}$
Thus, volume is maximum when $h=\sqrt{3}$
Now, maximum volume
$$ \begin{aligned} & V(\sqrt{3})=\frac{1}{3} \pi(9 \sqrt{3}-3 \sqrt{3}) \text { [from Eq. (ii)] } \\ = & 2 \sqrt{3} \pi \end{aligned} $$
