SATHEE: Application of Derivatives 1 Question 5

Application of Derivatives 1 Question 5

5. A helicopter is flying along the curve given by $y - x^{3 / 2} = 7, (x \geq 0)$ . A soldier positioned at the point $\frac{1}{2}, 7$ wants to shoot down the helicopter when it is nearest to him. Then, this nearest distance is

(2019 Main, 10 Jan II)

(a) $\frac{1}{3} \sqrt{\frac{7}{3}}$

(b) $\frac{\sqrt{5}}{6}$

(d) $\frac{1}{2}$

Show Answer

Answer:

Correct Answer: 5. (d)

Solution:

The helicopter is nearest to the soldier, if the tangent to the path, $y = x^{3 / 2} + 7, (x \geq 0)$ of helicopter at point $(x, y)$ is perpendicular to the line joining $(x, y)$ and the position of soldier $\frac{1}{2}, 7$ .

$∵$ Slope of tangent at point $(x, y)$ is

$\frac{d y}{d x} = \frac{3}{2} x^{1 / 2} = m_{1} (l e t)$

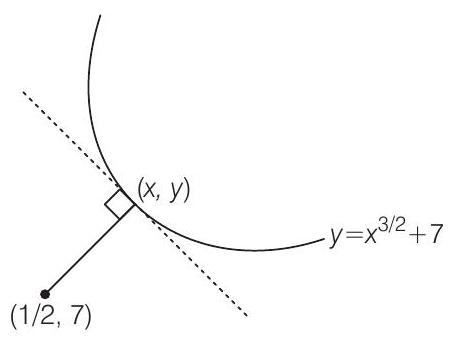
and slope of line joining $(x, y)$ and $\frac{1}{2}, 7$ is

$m_{2} = \frac{y - 7}{x - \frac{1}{2}}$

Now, $m_{1} \cdot m_{2} = - 1$

$\Rightarrow \frac{3}{2} x^{1 / 2} \frac{y - 7}{x - (1 / 2)} = - 1$

[from Eqs. (i) and (ii)]

$\Rightarrow \frac{3}{2} x^{1 / 2} \frac{x^{3 / 2}}{x - \frac{1}{2}} = - 1$

$[∵ y = x^{3 / 2} + 7]$

$\Rightarrow \frac{3}{2} x^{2} = - x + \frac{1}{2}$

$\Rightarrow 3 x^{2} + 2 x - 1 = 0$

$\Rightarrow 3 x^{2} + 3 x - x - 1 = 0$

$\Rightarrow 3 x (x + 1) - 1 (x + 1) = 0$

$\Rightarrow x = \frac{1}{3}, - 1$

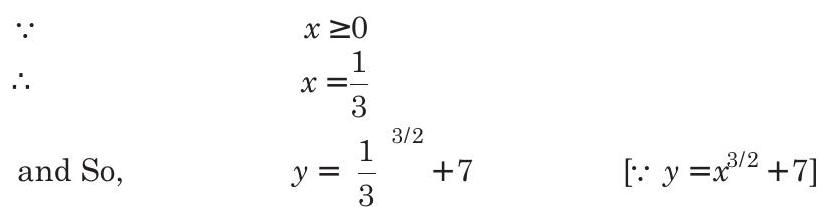
Thus, the nearest point is $\frac{1}{3}, {\frac{1}{3}}^{3 / 2} + 7$

Now, the nearest distance

$\begin{aligned} = \sqrt{\frac{1}{2} - {\frac{1}{3}}^{2} + 7 - {\frac{1}{3}}^{3 / 2} - 7} = \sqrt{{\frac{1}{6}}^{2} + {\frac{1}{3}}^{3}} \\ = \sqrt{\frac{1}{36} + \frac{1}{27}} = \sqrt{\frac{3 + 4}{108}} = \sqrt{\frac{7}{108}} = \frac{1}{6} \sqrt{\frac{7}{3}} \end{aligned}$